2020-09-24
160
(индуктивный элемент)
Пусть в цепь переменного тока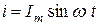 
включена индуктивность (рис. 3.8, а).
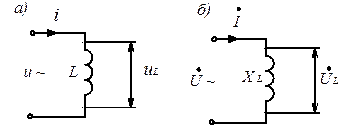
Рис. 3.8
Известно [1], что при прохождении тока через индуктивный элемент в нём возникает магнитный поток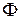 
, который наводит в нем ЭДС самоиндукции
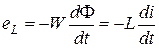, (3.12)
где W – число витков катушки индуктивности.
Эта ЭДС самоиндукции уравновешивается падением напряжения на индуктивности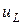 
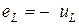(3.13)
Падение напряжения на индуктивности 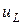с учётом (3.12) и (3.13) будет равно
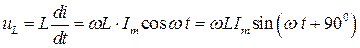(3.14)
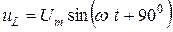
Введём понятие индуктивного сопротивления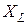 
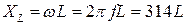, (Ом) (3.15)
где f = 50 Гц.
Графики изменения тока (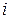
) и падения напряжения на катушке (
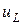) показаны на рис 3.9.
 |
Рис. 3.9
Из рис. 3.9 следует, что ток 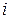и падение напряжения 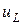колеблются в противофазе.
Построим векторную диаграмму для цепи, содержащей индуктивность L. Построение начинаем с комплексной плоскости (рис. 3.10). Параллельно оси действительных чисел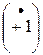 
строим вектор действующего значения тока 
.
 |
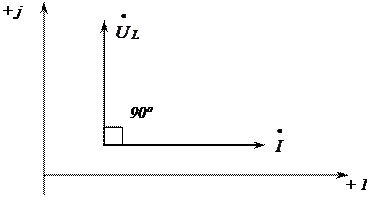Рис. 3.10
Теперь, сравнивая (рис. 3.9) законы изменения тока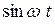 
и падения напряжения на индуктивности 
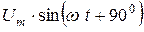, делаем вывод, что вектор падения напряжения на индуктивности 
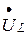опережает вектор тока 
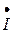на угол 
.
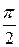Закон Ома в комплексном виде для индуктивного элемента запишется
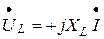, (3.16)
где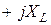 
– комплекс индуктивного сопротивления;
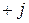показывает, что вектор 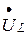опережает вектор 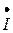на угол 
.
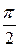Мгновенная мощность индуктивности равна:
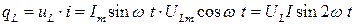(3.17)
Мощность в цепи, содержащей индуктивный элемент, называют реактивной индуктивной мощностью (+ QL) и измеряют в вольт-амперах реактивных (вар).
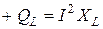(вар) (3.18)
