2020-09-24
97
Электроприемников – «треугольник»
«Треугольник» – это трехпроводная система, у которой начало последующей фазы соединено с концом предыдущей фазы и обозначается «Δ» (рис 4.8).
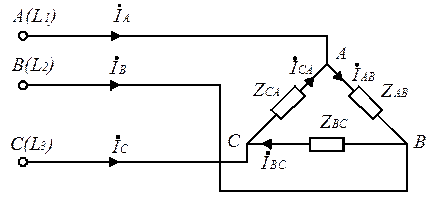
Рис. 4.8
Токи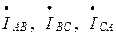 
называются фазными, а токи 
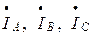– линейными.
Нетрудно заметить, что в «треугольнике» линейные и фазные напряжения равны.
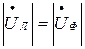. (4.17)
Найдём фазные токи из закона Ома:
; 
; 
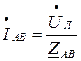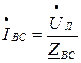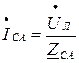
Линейные токи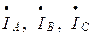 
определяются из I закона Кирхгофа:
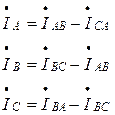(4.18)
Рассмотрим режим симметричной нагрузки, когда
, 
.
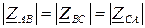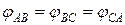Так как сопротивления равны, то равны по величине и фазные токи
.
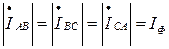Соответственно, между собой будут равны и линейные токи
.
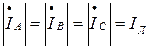Векторная диаграмма для симметричной резистивной нагрузки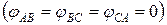 
показана на рис. 4.9.
Построение векторной диаграммы начинается с «треугольника» линейных (фазных) напряжений (А, В, С). Далее строим векторы фазных токов; так как нагрузка резистивная, то векторы фазных токов будут совпадать с векторами соответствующих фазных напряжений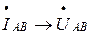 
, 
, 
.
|
|
|
 |
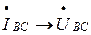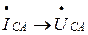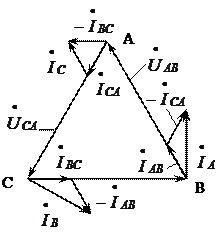Рис. 4.9
Векторы линейных токов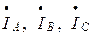 
строим с учетом (4.18). Ток 
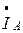строится следующим образом. Из конца вектора 
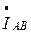параллельно вектору 
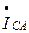строим вектор 
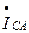, а затем соединяем конец вектора 
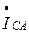с началом вектора 
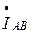– получаем вектор линейного тока 
.
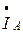Аналогичным образом строятся векторы линейных токов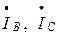 
.
С учетом векторной диаграммы основные электрические соотношения при симметричной нагрузке:
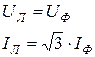(4.19)
При несимметричной нагрузке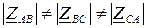 
, 
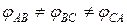, не будут равны и фазные токи 
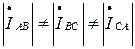и линейные токи 
.
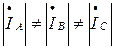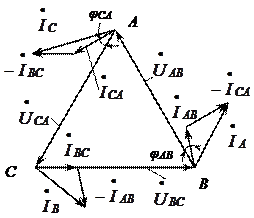Векторная диаграмма при несимметричной нагрузке 
, 
, 
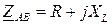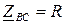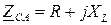показана на рис. 4.10.
Рис. 4.10
Основные электрические соотношения при несимметричной нагрузке:
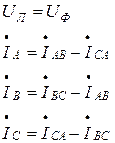(4.20)
