2020-09-24
161
Параллельное соединение электроприемников – основной вид соединений, так как в этом случае электроприёмники делаются на одно и то же напряжение.
Параллельное соединение – это такой вид соединения, когда на всех элементах одно и то же напряжение, а ток в неразветвлённой части равен геометрической сумме токов этих элементов согласно первому закону Кирхгофа.
Схема параллельного соединения R, xL, и xC приведена на рис. 3.16, а.
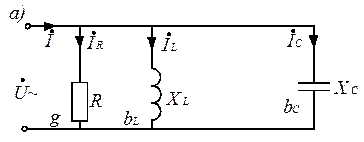
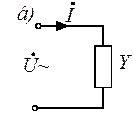
Рис. 3.16
Первый закон Кирхгофа в комплексном виде запишется следующим образом:
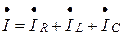(3.32)
Выразим токи из закона Ома:
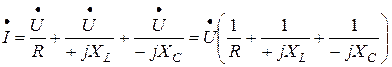(3.33)
Для параллельного соединения элементов вводится понятие проводимости, величины, обратной сопротивлению, измеряемой в сименсах:
· активная проводимость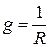 
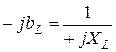(См);
·
|
(См);
· емкостная проводимость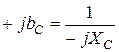 
(См).
С учётом (3.32) выражение (3.33) примет следующий вид:
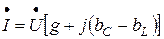(3.35)
Выражение в квадратных скобках обозначим через Y и назовем полной или комплексной, проводимостью:
|
|
|
|
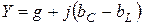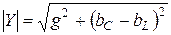(См)
(См)
Тогда закон Ома для параллельного соединения элементов в комплексном виде будет
|
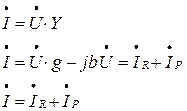
где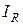 
– активная составляющая тока;
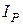– реактивная составляющая тока.
Этой форме записи закона Ома соответствует схема замещения, показанная на рис. 3.16.
Схемы а и б на рис. 3.16 являются эквивалентными.
Построим векторную диаграмму для параллельного соединения резистора, индуктивности и емкости.
Построение начинаем с комплексной плоскости (рис. 3.17, а). Параллельно оси действительных чисел (+ 1) строим вектор приложенного напряжения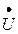 
, так как напряжение является общим для всех элементов. Далее по вектору напряжения 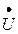строим вектор тока в резисторе 
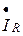(который совпадает по направлению с напряжением). Из конца вектора 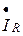строим вектор тока в конденсаторе 
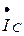(он опережает напряжение на угол 900). Из конца вектора 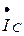строим вектор тока индуктивности 
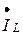(он отстает от напряжения на угол 900), получаем точку «а». Соединив точку «а» с началом вектора тока в резисторе 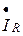, получаем вектор тока 
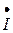в неразветвлённой части, при этом образуется треугольник токов. Угол 
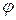между вектором напряжения 
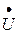и вектором тока 
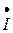соответствует углу сдвига фаз.
 | ||||||
 | ||||||
| ||||||
 | ||||||
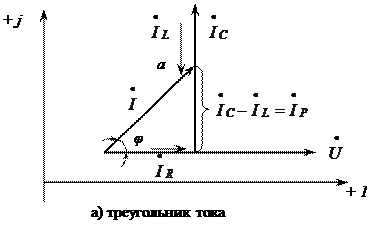Рис. 3.17
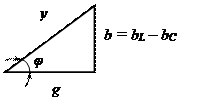
Если все стороны треугольника токов разделить на напряжение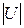 
, то получим подобный треугольнику токов треугольник проводимостей. Умножив стороны треугольника проводимостей на 
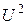, получаем треугольник мощностей.
Проанализировав закон Ома для последовательного соединения (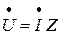
) и для параллельного соединения (
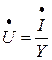), можно сделать вывод, что:
|
|
|
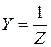. (3.38)
Соотношение (3.38) показывает, что для каждого последовательного соединения элементов существует эквивалентное параллельное соединение этих же элементов. И наоборот: для каждого параллельного соединения элементов существует эквивалентное последовательное соединение этих же элементов. Соотношение (3.38) широко используется для преобразования сложных электрических цепей.
