Под резонансным режимом электрической цепи, содержащей резистор R, индуктивность xL и емкость xC понимается такой режим, когда полное сопротивление цепи равняется активному, ток совпадает по фазе с напряжением (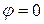 ) и коэффициент мощности (
) и коэффициент мощности (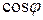 ) равен единице.
) равен единице.
Условия резонанса:
· при последовательном соединении Z = R, 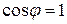 ,
, 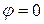 ;
;
· при параллельном – y = g, 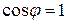 ,
, 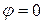 .
.
При последовательном соединении наблюдается резонанс напряжений, при параллельном соединении – резонанс тока.
Резонанс напряжений
Рассмотрим последовательное соединение резистора, индуктивности и ёмкости (рис. 3.18, а).
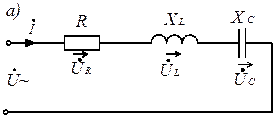
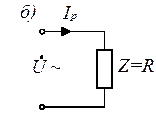
Рис. 3.18
Известно, что для последовательного соединения:
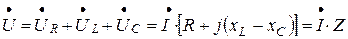
Так как 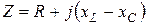 , то по условию резонанса
, то по условию резонанса 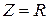 , а это будет, если
, а это будет, если 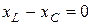 .
.
Тогда условием резонанса напряжений будет равенство индуктивного (xL) и ёмкостного (xC) сопротивлений.
xL = xC – условие резонанса напряжений.
Закон Ома для резонанса напряжений запишется в следующем виде:
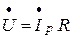 (3.40)
(3.40)
где 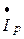 – ток при резонансе.
– ток при резонансе.
Этой форме записи закона Ома будет соответствовать схема замещения, показанная на рис. 3.18, б. Так как полное сопротивление 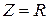 и достигает минимального значения, то резонансный ток (
и достигает минимального значения, то резонансный ток (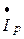 ) достигает максимального значения (
) достигает максимального значения (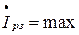 ). При этом наблюдается равенство падений напряжений на индуктивности
). При этом наблюдается равенство падений напряжений на индуктивности 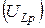 и ёмкости
и ёмкости 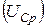 имеющих наибольшее значение.
имеющих наибольшее значение.
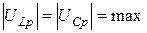 (3.41)
(3.41)
Равенство падений напряжений на индуктивности и ёмкости обусловило название этого явления – резонанс напряжений.
Резонансная частота, при которой наблюдается это явление, равна
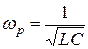 (3.42)
(3.42)
Из выражения (3.42) следуют следующие способы достижения резонанса напряжений:
1) изменением емкости (C = var);
2) изменением индуктивности (L = var);
3) изменением частоты питающей сети (f = var)(ω = 2 πf = var)
Остальные параметры должны оставаться неизменными. Зависимости некоторых параметров электрической цепи от емкости показаны на рис. 3.19.
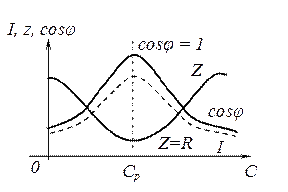
Рис. 3.19
Векторная диаграмма для резонансного режима показана на рис. 3.20. Построение производится аналогично разделу 3.6.
Из векторной диаграммы следует, что угол сдвига фаз 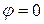 , тогда
, тогда 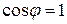 . При этом полная мощность S равняется активной мощности P и достигает наибольшего значения:
. При этом полная мощность S равняется активной мощности P и достигает наибольшего значения:
|
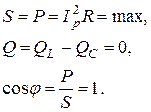
Из вышеизложенного можно сделать следующий вывод:
При резонансе напряжений электрическая цепь потребляет из сети наибольшую мощность, и падения напряжения на индуктивном и ёмкостном элементах достигают наибольшего значения, что увеличивает вероятность пробоя этих элементов, поэтому резонанс напряжений является нежелательным режимом работы электрической цепи.
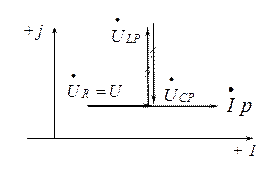
Рис. 3.20
Резонанс токов
Рассмотрим параллельное соединение реальной катушки индуктивности и ёмкости (рис. 3.21, а).
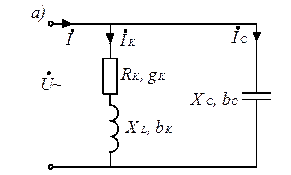
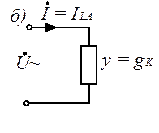
Рис. 3.21
Известно, что для параллельного соединения:
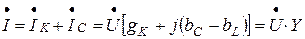 ,
,
где 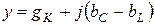 ;
; 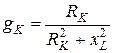 ;
; 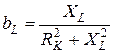 ;
; 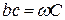 .
.
Так как по условию резонанса 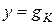 , то резонанс будет наблюдаться, когда
, то резонанс будет наблюдаться, когда 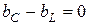 , поэтому условием резонанса тока будет равенство индуктивной (
, поэтому условием резонанса тока будет равенство индуктивной (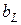 ) и емкостной (
) и емкостной (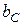 ) проводимостей.
) проводимостей.
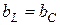 – условие резонанса (3.44)
– условие резонанса (3.44)
Из (3.44) следует равенство реактивной составляющей тока в индуктивности (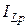 ) и емкости (
) и емкости (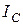 ), что и дало название этому явлению – резонанс токов.
), что и дало название этому явлению – резонанс токов.
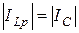 (3.45)
(3.45)
Поэтому ток в неразветвлённой части (I) будет равен активной составляющей тока индуктивности (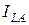 ) и достигает наименьшего значения.
) и достигает наименьшего значения.
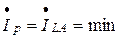 (3.46)
(3.46)
Закон Ома для резонанса токов запишется в следующем виде:
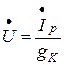 . (3.47)
. (3.47)
Этой форме записи закона Ома будет соответствовать схема замещения, показанная на рис. 3.21, б.
Резонансная частота равна
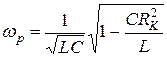 ,
,
при условии 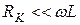 ,
, 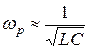 .
.
Способы достижения резонанса токов при условии 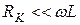 такие же, что и при резонансе напряжений.
такие же, что и при резонансе напряжений.
Зависимости некоторых параметров электрической цепи от емкости показаны на рис. 3.22.
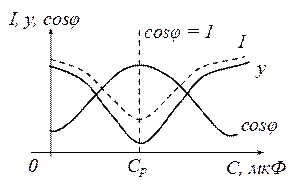
Рис. 3.22
Векторная диаграмма для резонанса токов показана на рис. 3.23, построение ее производится аналогично приведенному в разделе 3.7.
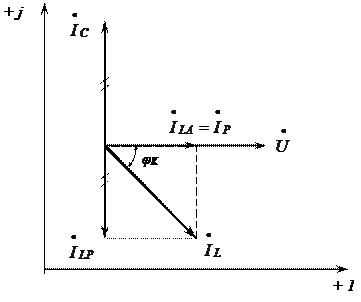 |
Рис. 3.23
Из векторной диаграммы следует, что угол сдвига фаз 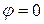 , поэтому коэффициент мощности
, поэтому коэффициент мощности 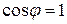 .
.
Реактивная мощность цепи равна нулю
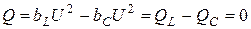 .
.
При этом индуктивная 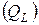 и емкостная
и емкостная 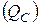 реактивные мощности могут приобретать весьма большие значения, оставаясь равными друг другу.
реактивные мощности могут приобретать весьма большие значения, оставаясь равными друг другу.
Полная мощность цепи при резонансе тока равна активной мощности и достигает наименьшего значения.
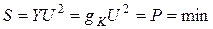 (3.48)
(3.48)
Коэффициент мощности всей цепи при резонансе токов
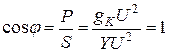 .
.
При резонансе токов электрическая цепь потребляет минимальную мощность от источника, поэтому такой режим работы электрической цепи является желательным.
3.9. Способ повышения коэффициента мощности 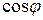 электроприёмника
электроприёмника
Электроприёмники (рис. 3.24) в своём большинстве обладают активно-индуктивными свойствами (электродвигатели, трансформаторы) и поэтому обладают низким коэффициентом мощности.
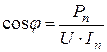 , (3.49)
, (3.49)
где 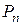 – мощность электроприемника, кВт;
– мощность электроприемника, кВт;
U – напряжение питающей сети, В;
Iп – ток электроприёмника, А.
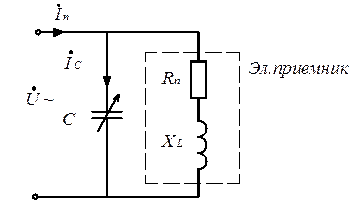
Рис. 3.24
Из (3.49) следует, что ток приёмника Iп равен
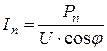 . (3.50)
. (3.50)
При постоянной мощности (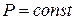 ) и напряжении (
) и напряжении (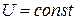 ), потребляемый ток Iп будет зависеть от величины коэффициента мощности
), потребляемый ток Iп будет зависеть от величины коэффициента мощности 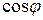 .
.
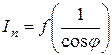 . (3.51)
. (3.51)
Чем ниже коэффициент мощности 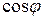 , тем больший ток Iп потребляет электроприёмник.
, тем больший ток Iп потребляет электроприёмник.
Повышение 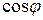 называется компенсацией угла сдвига фаз
называется компенсацией угла сдвига фаз 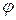 , это произойдёт при подключении параллельно электроприёмнику конденсатора С, при этом используется режим, близкий к режиму резонанса токов.
, это произойдёт при подключении параллельно электроприёмнику конденсатора С, при этом используется режим, близкий к режиму резонанса токов.
Построение векторной диаграммы электроприёмника до и после подключения конденсатора показано на рис.3.25.
а) до подключения конденсатора б) после подключения конденсатора
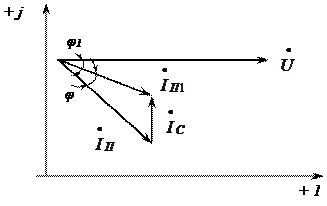 | |||
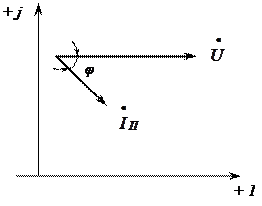 | |||
Рис. 3.25
Зависимости тока приёмника Iп и коэффициента мощности 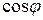 от величины емкости конденсатора приведены на рис. 3.26.
от величины емкости конденсатора приведены на рис. 3.26.
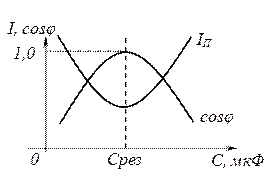
Рис. 3.26
Из рисунков 3.25 и 3.26 следует, что подключение конденсатора снижает потребляемый ток и повышает 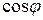 электроприёмника, особенно когда емкость конденсатора равна емкости, соответствующей резонансу токов.
электроприёмника, особенно когда емкость конденсатора равна емкости, соответствующей резонансу токов.
Нормируемое значение коэффициента мощности в энергосистемах составляет 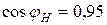 . Величину емкости конденсатора, необходимого для подключения к электроприемнику и повышения
. Величину емкости конденсатора, необходимого для подключения к электроприемнику и повышения 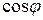 до нормируемого значения, можно определить из следующего выражения:
до нормируемого значения, можно определить из следующего выражения:
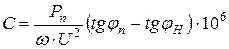 (мкф) (3.52)
(мкф) (3.52)
где 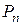 – мощность потребителя, кВт;
– мощность потребителя, кВт;
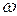 – угловая частота тока, 1/с;
– угловая частота тока, 1/с; 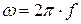 ;
;
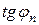 – тангенс угла сдвига фаз
– тангенс угла сдвига фаз 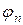 , соответствующий
, соответствующий 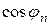 ;
;
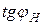 – тангенс угла сдвига фаз
– тангенс угла сдвига фаз 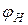 , соответствующий
, соответствующий 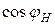 (
(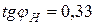 ).
).
 2020-09-24
2020-09-24 114
114








