Схема соединения «звезда» с нулевым (нейтральным) проводом (четырёхпроводная) показана на рис. 4.3.
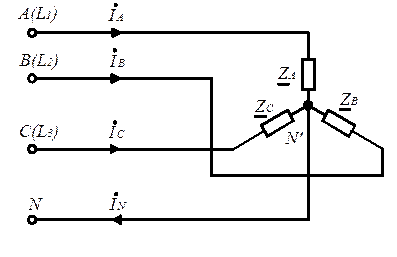
Рис. 4.3
Определим фазные токи из закона Ома:
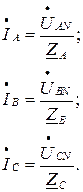 (4.7)
(4.7)
Ток в нейтральном проводе
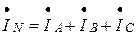 .
.
Необходимо отметить, что в трёхфазных цепях режим работы каждой фазы не зависит от режима работы других фаз за исключением аварийных режимов.
Рассмотрим симметричный режим работы цепи, когда сопротивления в фазах одинаковы, равны по величине и имеют одинаковый угол сдвига фаз
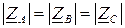 ,
, 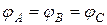 .
.
Так как источник выдаёт симметричные системы фазных и линейных напряжений, то
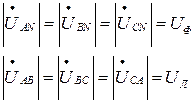
С учетом (4.7) будут равны между собой фазные и линейные токи
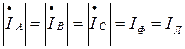
Электрические соотношения в «звезде» с учетом (4.6) при симметричной нагрузке
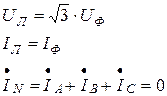 (4.8)
(4.8)
Построим векторную диаграмму для симметричной резистивной нагрузки (рис. 4.4).
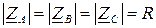 ,
, 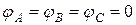 .
.
Построение векторной диаграммы производится аналогично рис. 4.2. Так как нагрузка резистивная, то векторы фазных токов совпадают с соответствующими векторами фазных напряжений
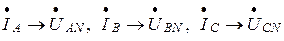 .
.
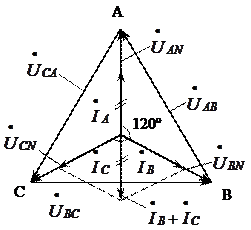 |
Рис. 4.4
Сложив векторы 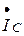 и
и 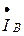 , получим вектор суммарного тока, который равен по величине вектору
, получим вектор суммарного тока, который равен по величине вектору 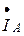 и направлен против него, поэтому ток в нейтральном проводе равен нулю
и направлен против него, поэтому ток в нейтральном проводе равен нулю 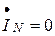 .
.
При несимметричной нагрузке 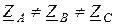 соответствующие фазные и линейные токи не будут равны между собой
соответствующие фазные и линейные токи не будут равны между собой
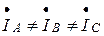
Электрические соотношения в «звезде» с учётом (4.6) при несимметричной нагрузке:
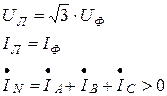 (4.9)
(4.9)
Векторная диаграмма для несимметричной нагрузки показана на рис. 4.5
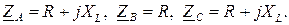
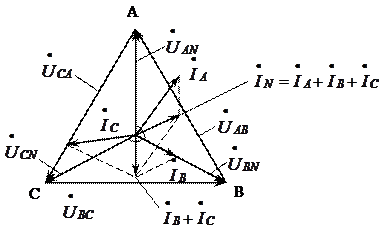 |
Рис. 4.5
Рассмотрим режимы работы трёхфазной цепи при обрыве нейтрального провода – трёхпроводная «звезда» (рис. 4.6).
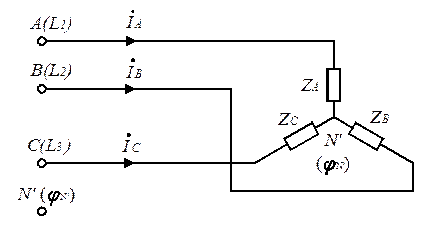
Рис. 4.6
При симметричном режиме 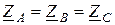 известно, что при четырёхпроводной системе ток в нейтральном проводе равен нулю
известно, что при четырёхпроводной системе ток в нейтральном проводе равен нулю 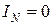 , поэтому отсутствие нейтрального провода NN’ не влияет на режим работы и электрические соотношения запишутся следующим образом:
, поэтому отсутствие нейтрального провода NN’ не влияет на режим работы и электрические соотношения запишутся следующим образом:
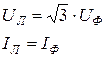 (4.10)
(4.10)
При несимметричной нагрузке 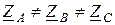 в четырёхпроводной системе по нейтральному проводу NN’ идет ток
в четырёхпроводной системе по нейтральному проводу NN’ идет ток 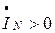 , который обусловлен разностью потенциалов между нейтральной точкой источника N и приёмника N’
, который обусловлен разностью потенциалов между нейтральной точкой источника N и приёмника N’
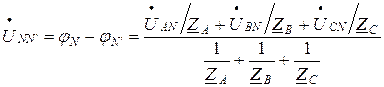 (4.11)
(4.11)
При наличии нейтрального провода и при несимметричной нагрузке 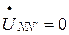 .
.
При несимметричной нагрузке и трёхпроводной системе 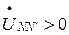 , тогда напряжение на каждой фазе электроприёмника:
, тогда напряжение на каждой фазе электроприёмника:
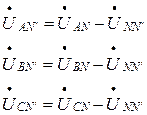 (4.13)
(4.13)
Поэтому происходит сдвиг нейтральной точки приемника N’ относительно нейтральной точки источника N и фазные напряжения не равны между собой
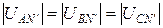 (4.14)
(4.14)
Симметрия линейных напряжений сохраняется
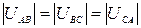 (4.15)
(4.15)
Векторная диаграмма для несимметричной резистивной нагрузки 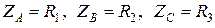 показана на рис. 4.7.
показана на рис. 4.7.
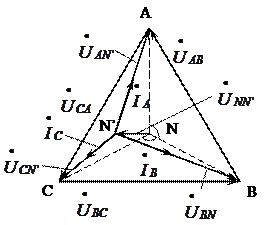 |
Рис. 4.7
Построение начинаем со штрихпунктирной «звезды» симметричных фазных напряжений источника. Затем строим вектор нулевого напряжения 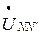 и, соединив точку N’ с точками А, В, С, получаем векторы фазных напряжений приемника
и, соединив точку N’ с точками А, В, С, получаем векторы фазных напряжений приемника 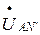 ,
, 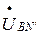 ,
, 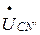 .
.
В случае резистивной нагрузки, векторы соответствующих фазных токов будут направлены по векторам фазных напряжений 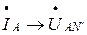 ,
, 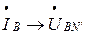 ,
, 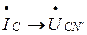 . Соединив точки А, В, С между собой, получим «треугольник» линейных напряжений
. Соединив точки А, В, С между собой, получим «треугольник» линейных напряжений 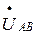 ,
, 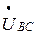 ,
, 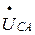 .
.
Основные электрические соотношения в трехпроводной «звезде» и несимметричной нагрузке:
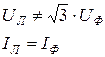 (4.16)
(4.16)
Для симметрии линейных и фазных напряжений (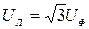 ) присутствие нейтрального провода (NN’) при несимметричной нагрузке является обязательным.
) присутствие нейтрального провода (NN’) при несимметричной нагрузке является обязательным.
 2020-09-24
2020-09-24 133
133








