Задания
1. Найти площадь фигуры, ограниченной кривыми:
1) в прямоугольных координатах;
2) кривая задана в параметрическом виде;
3) в полярных координатах.
2. Найти длину дуги плоской кривой, заданной:
1) в прямоугольных координатах;
2) в полярных координатах.
3. Найти объем тела, образованного при вращении фигуры, ограниченной данными кривыми.
Вариант 1
1. 1)  . 2)
. 2)  . 3.
. 3. 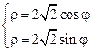 .
.
2. 1) 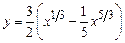 ,
, 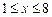 . 2)
. 2) 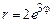 ,
, 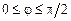 .
.
3. 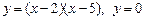 , вокруг оси
, вокруг оси 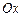 .
.
Вариант 2
1. 1) 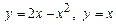 . 2)
. 2) 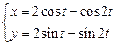 . 3)
. 3) 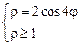 .
.
2. 1) 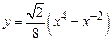 ,
, 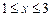 . 2)
. 2)  ,
, 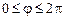 .
.
3. 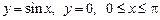 , вокруг оси
, вокруг оси 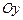 .
.
Вариант 3
1. 1)  . 2)
. 2) 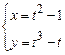 . 3)
. 3)  .
.
2. 1)  ,
, 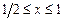 . 2)
. 2) 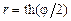 ,
, 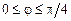 .
.
3.  , вокруг оси
, вокруг оси 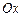 .
.
Вариант 4
1. 1)  . 2)
. 2)  .
.
3)  .
.
2. 1) 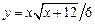 ,
, 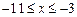 . 2)
. 2) 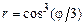 .
.
3. 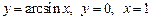 , вокруг оси
, вокруг оси 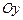 .
.
Вариант 5
1. 1) 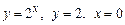 . 2)
. 2) 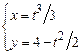 . 3)
. 3) 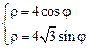 .
.
2. 1)  , отсеченной осью
, отсеченной осью 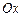 .
.
2) 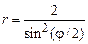 ,
, 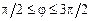 .
.
3. 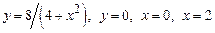 , вокруг оси
, вокруг оси 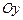 .
.
Вариант 6
1. 1) 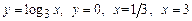 . 2)
. 2)  ,
, 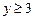 .
.
3) 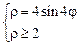 .
.
2. 1) 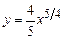 ,
,  . 2)
. 2)  ,
, 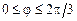 .
.
3. 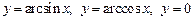 , вокруг оси
, вокруг оси 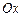 .
.
Вариант 7
1. 1) 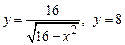 . 2)
. 2) 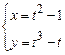 . 3)
. 3) 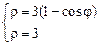 .
.
2. 1) 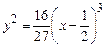 ,
,  . 2)
. 2) 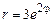 ,
, 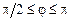 .
.
3.  , вокруг оси
, вокруг оси 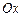 .
.
Вариант 8
1. 1) 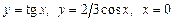 . 2)
. 2) 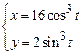 ,
, 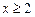 .
.
3) 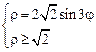 .
.
2. 1) 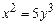 ,
, 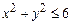 . 2)
. 2) 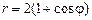 ,
, 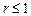 .
.
3.  , вокруг оси
, вокруг оси 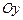 .
.
Вариант 9
1. 1)  . 2)
. 2)  . 3)
. 3) 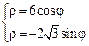 .
.
2. 1) 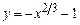 ,
, 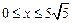 . 2)
. 2) 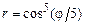 .
.
3. 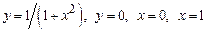 , вокруг оси
, вокруг оси 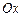 .
.
Вариант 10
1. 1) 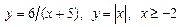 . 2)
. 2)  .
.
3) 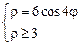 .
.
2. 1)  ,
, 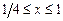 . 2)
. 2) 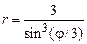 .
.
3. 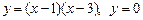 , вокруг оси
, вокруг оси 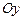 .
.
Вариант 11
1. 1) 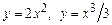 . 2)
. 2) 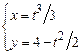 ,
, 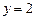 .
.
3) 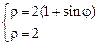 .
.
2. 1) 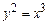 , отсеченной прямой
, отсеченной прямой 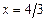 .
.
2)  ,
, 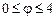 .
.
3. 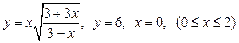 , вокруг оси
, вокруг оси 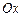 .
.
Вариант 12
1. 1) 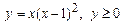 . 2)
. 2) 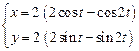 .
.
3) 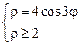 .
.
2. 1) 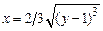 ,
, 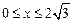 .
.
2) 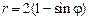 ,
,  .
.
3. 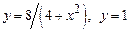 , вокруг оси
, вокруг оси 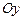 .
.
Вариант 13
1. 1) 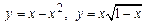 .
.
2) 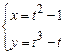 .
.
3)  .
.
2. 1) 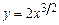 ,
, 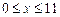 . 2)
. 2) 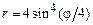 .
.
3. 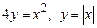 , вокруг оси
, вокруг оси 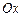 .
.
Вариант 14
1. 1) 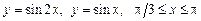 .
.
2) 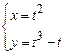 .
.
3)  .
.
2.1) 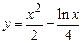 ,
, 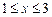 . 2)
. 2) 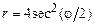 ,
, 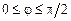 .
.
3. 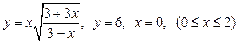 , вокруг оси
, вокруг оси 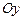 .
.
Вариант 15
1. 1) 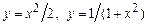 .
.
2) 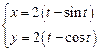 .
.
3) 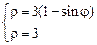 .
.
2. 1) 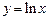 ,
,  . 2)
. 2)  ,
, 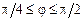 .
.
3.  , вокруг оси
, вокруг оси 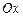 .
.
Вариант 16
1. 1) 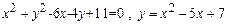 .
.
2)  . 3)
. 3) 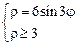 .
.
2. 1)  , отсеченной прямой
, отсеченной прямой 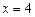 .
.
2) 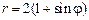 ,
, 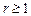 .
.
3. 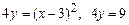 , вокруг оси
, вокруг оси 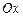 .
.
Вариант 17
1. 1) 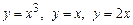 .
.
2) 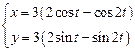 . 3)
. 3) 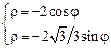 .
.
2. 1) 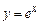 ,
, 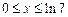 . 2)
. 2)  .
.
3. 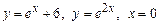 , вокруг оси
, вокруг оси 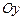 .
.
Вариант 18
1. 1) 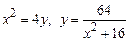 .
.
2) 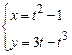 . 3)
. 3)  .
.
2. 1) 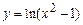 ,
, 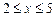 . 2)
. 2) 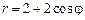 ,
, 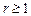 .
.
3. 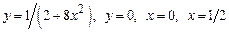 , вокруг оси
, вокруг оси 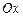 .
.
Вариант 19
1. 1) 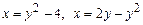 .
.
2)  . 3)
. 3) 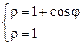 .
.
2. 1) 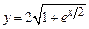 ,
, 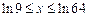 . 2)
. 2) 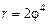 ,
, 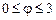 .
.
3. 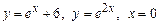 , вокруг оси
, вокруг оси 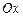 .
.
Вариант 20
1. 1) 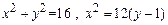 .
.
2) 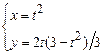 . 3)
. 3) 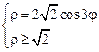 .
.
2. 1) 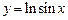 ,
, 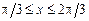 . 2)
. 2)  .
.
3. 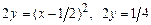 , вокруг оси
, вокруг оси 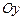 .
.
Вариант 21
1. 1)  .
.
2) 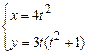 ,
, 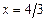 . 3)
. 3) 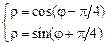 .
.
2. 1) 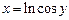 ,
,  . 2)
. 2) 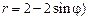 ,
, 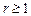 .
.
3. 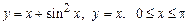 , вокруг оси
, вокруг оси 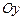 .
.
Вариант 22
1. 1) 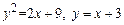 .
.
2) 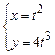 ,
, 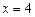 . 3)
. 3) 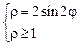 .
.
2. 1)  ,
, 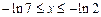 .
.
2)  ,
,  .
.
3. 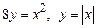 , вокруг оси
, вокруг оси 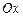 .
.
Вариант 23
1. 1) 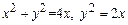 .
.
2) 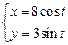 ,
,  . 3)
. 3) 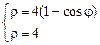 .
.
2. 1)  , отсеченной прямой
, отсеченной прямой 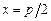 . 2)
. 2) 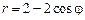 .
.
3. 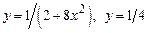 , вокруг оси
, вокруг оси 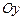 .
.
Вариант 24
1. 1)  .
.
2) 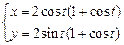 . 3)
. 3) 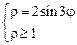 .
.
2. 1) 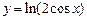 ,
, 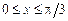 . 2). 2)
. 2). 2) 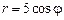 .
.
3. 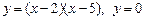 , вокруг оси
, вокруг оси 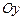 .
.
Вариант 25
1. 1) 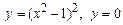 .
.
2)  . 3)
. 3) 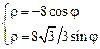 .
.
2. 1) 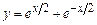 , от
, от 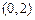 до
до 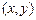 . 2)
. 2) 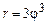 ,
, 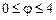 .
.
3. 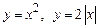 , вокруг оси
, вокруг оси 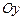 .
.
Вариант 26
1. 1) 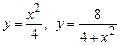 . 2)
. 2) 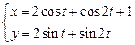 .
.
3) 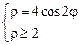 .
.
2. 1) 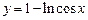 ,
, 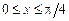 . 2)
. 2) 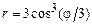 .
.
3.  , вокруг оси
, вокруг оси 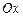 .
.
Вариант 27
1. 1) 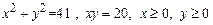 .
.
2) 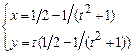 .
.
3) 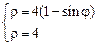 .
.
2. 1)  ,
, 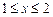 . 2)
. 2) 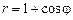 ,
, 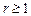 .
.
3. 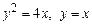 , вокруг оси
, вокруг оси 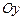 .
.
Вариант 28
1. 1) 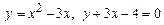 .
.
2) 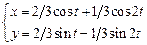 .
.
3) 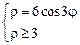 .
.
2. 1) 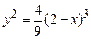 , отсеченной прямой
, отсеченной прямой  .
.
2) 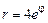 ,
, 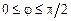 .
.
3. 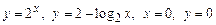 , вокруг оси
, вокруг оси 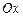 .
.
Ч А С Т Ь III
ПРИЛОЖЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
К РЕШЕНИЮ ФИЗИЧЕСКИХ ЗАДАЧ.
ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
СПРАВОЧНЫЙ МАТЕРИАЛ
Путь, пройденный точкой. Если точка движется по некоторой кривой и абсолютная величина скорости ее v = f (t) есть известная функция времени t, то путь, пройденный точкой за промежуток времени [ 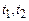 ], равен
], равен
 .
.
Пример 1. Скорость точки равна 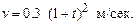 Найти путь s, пройденный точкой за промежуток времени Т = 9 с, протекший от начала движения. Чему равна средняя скорость движения за этот промежуток?
Найти путь s, пройденный точкой за промежуток времени Т = 9 с, протекший от начала движения. Чему равна средняя скорость движения за этот промежуток?
Решение. Имеем
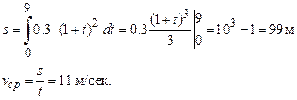
Работа силы. Если переменная сила F = f (x) действует в направлении оси ОХ, то работа силы на отрезке [ 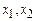 ] равна
] равна
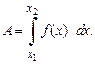
 Давление жидкости. Для вычисления силы давления жидкости используют закон Паскаля, согласно которому сила давления жидкости на площадку S с глубиной погружения h равна
Давление жидкости. Для вычисления силы давления жидкости используют закон Паскаля, согласно которому сила давления жидкости на площадку S с глубиной погружения h равна
 P = g h S,
P = g h S,
где g – удельный вес жидкости.
Пример 2. Найти силу давления, испытываемую полукругом радиуса r, погруженным вертикально в воду так, что его диаметр совпадает с поверхностью воды (рис. 3.1)
Решение. Разбиваем площадь полукруга на элементы - полоски, параллельные поверхности воды.
Площадь одного такого элемента (отбрасывая б.м. высшего порядка), находящегося на 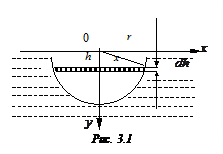 расстоянии h от поверхности,
расстоянии h от поверхности,
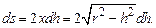
Сила давления, испытываемая этим элементом, равна
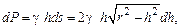 где g – удельный вес жидкости, равный единице.
где g – удельный вес жидкости, равный единице.
Отсюда вся сила давления есть
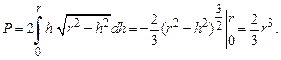
Кинетическая энергия. Кинетической энергией материальной точки, имеющей массу m и обладающей скоростью v, называется выражение

Кинетическая энергия системы n материальных точек с массами  , обладающих соответственно скоростями
, обладающих соответственно скоростями 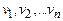 , равна
, равна
 (3.1)
(3.1)
Для подсчета кинетической энергии тела его надлежащим образом разбивают на элементарные частицы (играющие роль материальных точек), а затем, суммируя кинетические энергии этих частиц, в пределе вместо суммы (3.1) получают интеграл.
 2020-09-24
2020-09-24 110
110








