2020-09-24
116
Теорема Кронекера-Капелли. Для того, чтобы система линейных уравнений имела хотя бы одно решение необходимо и достаточно, чтобы ранг от матрицы этой системы совпадал c рангом её расширенной матрицы (т.е. матрицы, в которой справа как её часть записаны свободные члены).
· Совместная система имеет хотя бы одно решение.
· Несовместная система – решений не имеет.
Система, в которой все свободные члены равны 0 называется приведённой.
Теорема. Если ранг матрицы приведённой системы равен r, то эта система имеет (n-r) линейно-независимых решений.
Любой набор из (n-r) линейно-независимых решений приведённой системы называется фундаментальной системой решений.
Теорема. Пусть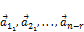 
образует фундаментальную систему решений, тогда для любых констант 
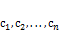линейная комбинация 
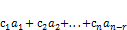также является решением приведённой системы.
И наоборот, на всякое решение приведённой системы существует константы 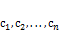, где векторы 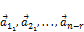– это фундаментальная система решений.
Общее решение неоднородной системы линейных уравнений. Теорема
, 
, 
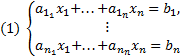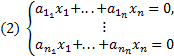
Теорема: Пусть векторы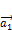 
, 
, 
…, 
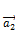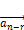образуют фундаментальную систему решений приведённой системы (2), а вектор 
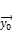является некоторым частным решением неоднородной системы (1), тогда общее решение неоднородной системы (1) задаётся вектором (3) 
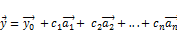для всех 
, 
, … 
∈ ℝ.
И наоборот для любого решения неоднородной системы (1) существует константы , , … 
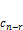∈ ℝ такие что это решение представлено в виде (3), где 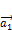, , 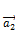…, 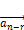— это фундаментальная система решений приведённой системы (2).
