2020-09-24
89
Теорема 1: для того, чтобы однородная система (1) имела нетривиальное решение необходимо и достаточно, чтобы определитель матрицы системы A был равен 0.
Теорема 2: если определитель A однородной системы (1) не равен 0, то эта система имеет тривиальные решения.
Рассмотрим поле скаляров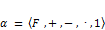 
. Например: 
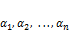— n-мерный вектор из n элементов множества F, записанных в столбец 
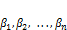-векторов.
Будем называть векторы равными, если их соответствующие компоненты равны между собой.
Пусть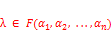 
, тогда под умножением скаляров 
на вектор…
Множество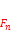 
c введёнными на этом множестве операциями сложения и умножения на скаляр называют арифметическим двумерным пространством.
Система векторов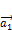 
, 
, 
…, 
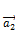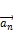называется линейно-зависимой если существует одновременно не равные нулю константы 
, 
, … 
такие, что линейная комбинация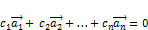 
Система векторов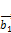 
, 
, …, 
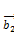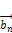называется линейно-независимой если существует одновременно не равные нулю константы , , … такие, что линейная комбинация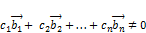 
.
Теорема 3: система векторов, содержащая нулевой вектор, является линейно-зависимой.
Теорема 4: если система векторов содержит линейно-зависимую подсистему, то вся система является линейно-зависимой.
