2020-09-24
147
Подматрица матрицы A – матрица, полученная из матрицы A, путём удаления из неё строки i и столбца j.
Подматрица k-ого порядка – подматрица размерности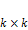 
.
Минор k-ого порядка – определитель подматрицы k-ого порядка.
Алгебраическое дополнение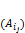 
– соответствующий минор, взятый со знаком, определяемым по формуле (-1)i+j.
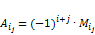
Теорема 1. Если в квадратной матрице A элементы в последней строке быть может за исключением элементы 
равны нулю, то определитель высчитывается по формуле: 
.
Теорема 2. Если в квадратной матрице A элементы в какой-либо строке за исключением одного элементы равны нулю, то определитель высчитывается по формуле: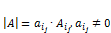 
.
При разложении определителя квадратной матрицы по элементам выбранной строки(столбца) следует учитывать эти две теоремы:
Теорема 1. Пусть дана 
, тогда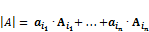 
.
Замечание. Теорема остаётся верной и при разложении по j (т.е. по строкам).
Теорема 2. Сумма произведений элементов одной из строк на алгебраические дополнения другой строки равна 0.
Определитель произведения двух квадратных матриц. Теорема
|
|
|
Теорема. Определитель произведения двух квадратных матриц равен произведению определителей сомножителей.
Сведение неоднородной системы линейных уравнений к матричному уравнению
, где 
– свободные члены
Если все не обращаются в 0, то система называется неоднородной, если все обращаются в 0, то система называется однородной
Поэтапно:
1. 
(1), где 
, 
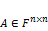, а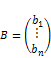 
.
2. С учётом введённых обозначений изначальную систему можно представить в виде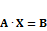 
(1).
3. Пусть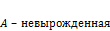 
(т.е. её определитель не равен 0), тогда для A существует обратная матрица (
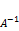). Умножим обе части уравнения (1) на : 
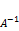4. 
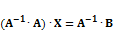
5. 
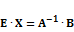
6. 
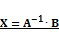(это один из методов, его следует запомнить)
Метод Крамера решения неоднородных систем линейных уравнений
Теорема. Если определитель матрицы системы уравнений А (1) не равен 0, то решение можно найти по формулам Крамера.
, 
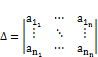, где свободные члены b встают на место строки i
