Критерий компланарности вектора и плоскости. Теорема

Теорема. Пусть относительно прямоугольно-декартовой системы координат заданы вектор  и плоскость, заданная (2). Тогда необходимое и достаточное условие компланарности вектора  и данной плоскости имеет вид:

Доказательство:

· Отложим вектор  от произвольной точки 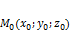 заданной плоскости.

· Конец Р отложенного вектора будет иметь координаты .

· Вектор коллинеарен заданной плоскости тогда и только тогда, когда точка Р лежит в данной плоскости, т.е. выполняется уравнение (2):

.

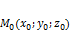·  лежит в плоскости, следовательно, .

· После раскрытия скобок с учётом уравнения выше остаётся условие:

.

Из этой теоремы следует, что главный вектор плоскости , заданной общим уравнением плоскости относительно общей декартовой системы координат, не компланарен этой плоскости: .

Уравнение плоскости, проходящей через 2 заданные точки и компланарной ненулевому вектору. Теоремы 1-3

Теорема. Пусть относительно прямоугольно-декартовой системы координат заданы две точки  и  и ненулевой вектор , компланарный плоскости . Тогда уравнение плоскости имеет вид:

Доказательство:

· Пусть три точки ,  точка с координатами , а также  лежат на .

· Векторы с координатами ,   и вектор  компланарны.

· Следовательно, матрица из их координат равняется 0.

Обратная теорема. Всякое решение уравнения (1) определяет точку с координатами , лежащую на плоскости.

Теорема: Пусть относительно прямоугольно-декартовой системы координат заданы 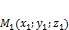, , 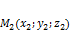. Тогда уравнение плоскости, проходящей через три точки, не лежащие на одной прямой:

Доказательство:

· Пусть , ,  лежат на одной плоскости.

· Возьмём произвольным образом точку 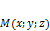, лежащую на плоскости, тогда векторы , , коллинеарны, так как лежат в одной плоскости.

· Следовательно, определитель, составленный из их координат, равен 0 ч.т.д.

Обратная теорема. Всякое решение уравнения (2) определяет точку, лежащую на плоскости.