Пусть относительно прямоугольно-декартовой системы координат заданы:
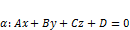 и
и 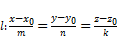
Углом между плоскостью  и прямой
и прямой  называют угол между этой прямой и её ортогональной проекцией на плоскость
называют угол между этой прямой и её ортогональной проекцией на плоскость  . Справедлива формула:
. Справедлива формула:
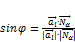 (
(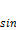 , потому что берётся угол не между прямой и вектором плоскости, а угол между прямой и её проекцией на плоскость).
, потому что берётся угол не между прямой и вектором плоскости, а угол между прямой и её проекцией на плоскость).
Из этой формулы следует, что:
1. 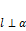 , когда
, когда 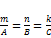 ;
;
2. 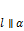 , когда
, когда 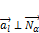 .
.
Кривые второго порядка (на плоскости): Окружность. Эллипс. Каноническое уравнение эллипса. Гипербола. Каноническое уравнение гиперболы. Парабола. Каноническое уравнение параболы
Говорят, что на плоскости задана кривая, если координаты точек, лежащие на этой кривой, удовлетворяют  .
.
Кривыми второго порядка на плоскости называют линии, координаты точек которых удовлетворяют
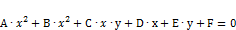 , где
, где 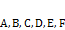 – действительные числа, при чём
– действительные числа, при чём 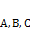 одновременно в ноль не обращаются.
одновременно в ноль не обращаются.
| Кривая второго порядка | Определение | Дополнительные характеристики | Каноническое уравнение |
| Окружность | Геометрическое место точек на плоскости, для каждой из которых расстояние до заданной точки есть постоянная величина, большая, чем ноль, и равная  . .
| 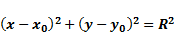 , ,
 – радиус окружности, – радиус окружности,
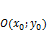 – центр окружности.
Если O совпадает с (0;0), то уравнение принимает вид: x2+y2=R2 – центр окружности.
Если O совпадает с (0;0), то уравнение принимает вид: x2+y2=R2
| |
| Эллипс | Геометрическое место точек на плоскости, для которых сумма расстояний до двух заданных точек 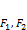 (фокусов) есть величина постоянная, равная (фокусов) есть величина постоянная, равная 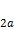 (или 2 (или 2  ) и большая, чем расстояние между фокусами: ) и большая, чем расстояние между фокусами: 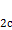 . .
| 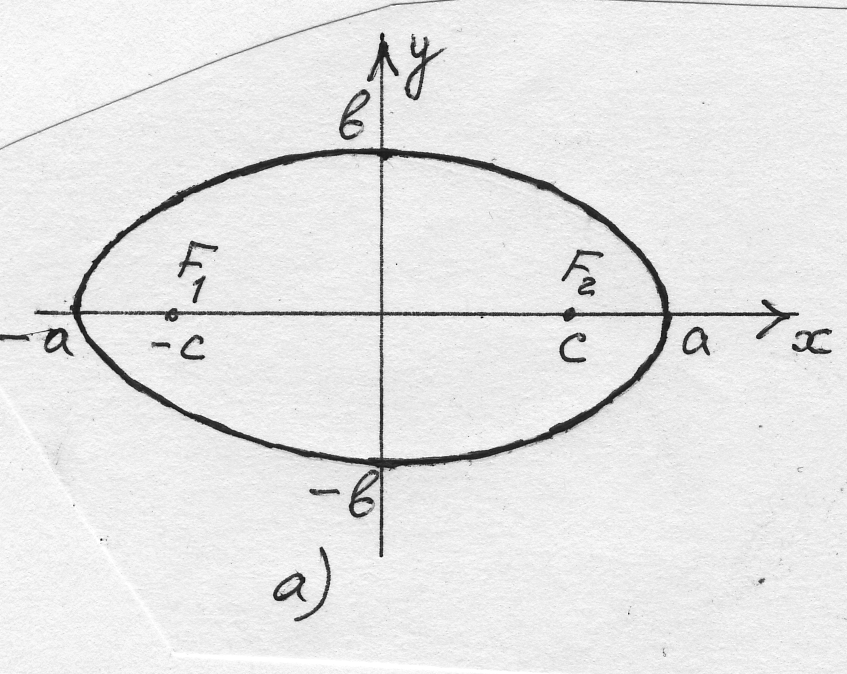 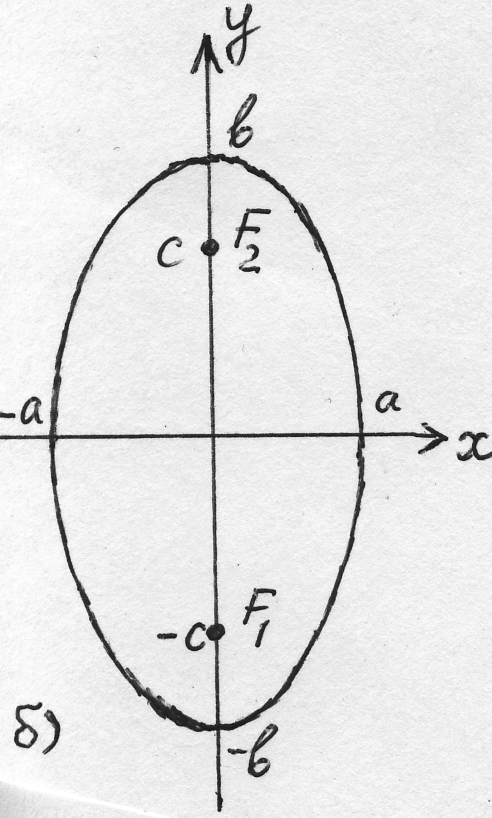 a) При
a) При 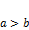 фокусы лежат на оси фокусы лежат на оси 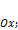
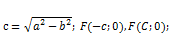 б) При
б) При 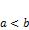 фокусы лежат на оси фокусы лежат на оси 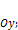
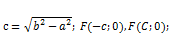 Эксцентриситетом эллипса называют степень сжатости эллипса
Эксцентриситетом эллипса называют степень сжатости эллипса 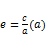 или или 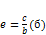 . 0<e<1 . 0<e<1
| 
|
| Парабола | Геометрическое место точек на плоскости, равноудалённых от заданной точки, называемой фокусом параболы и до прямой, называемой директрисой параболы. | 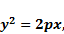 где
где  – параметр параболы, равный расстоянию от фокуса до директрисы параболы.
Так как p>0, то и x>0. – параметр параболы, равный расстоянию от фокуса до директрисы параболы.
Так как p>0, то и x>0.
| |
| Гипербола | Геометрическое место точек, разность от каждой из которых до двух данных точек 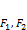 , называемых фокусами, есть величина постоянная, равная , называемых фокусами, есть величина постоянная, равная 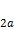 уточнить уточнить
| уточнить | 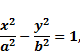
|
 2020-09-24
2020-09-24 85
85








