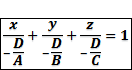
Доказательство:
· 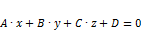
· 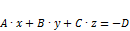
· 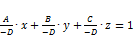
· 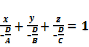
Плоскость пересекает координатные оси в точках с координатами 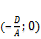 ,
, 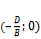 ,
, 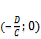 .
.
Параметрические уравнения плоскости. Теорема
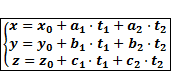
Доказательство:
· Пусть 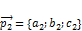 и
и 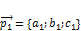 компланарны плоскости, а
компланарны плоскости, а 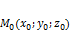 лежит на этой плоскости.
лежит на этой плоскости.
· Выберем на плоскости произвольную точку 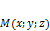 .
.
· 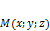 лежит на плоскости только тогда, когда
лежит на плоскости только тогда, когда 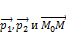 – компланарны.
– компланарны.
· Если 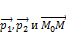 – компланарны, то их можно выразить через друг друга:
– компланарны, то их можно выразить через друг друга:
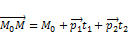
· Записав разложение вектора 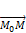 по координатам получаем параметрическое уравнение прямой.
по координатам получаем параметрическое уравнение прямой.
Частные случаи расположения плоскости относительно прямоугольно-декартовой системы координат. Теорема
Теорема. Пусть дана плоскость 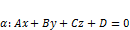 . Тогда:
. Тогда:
· 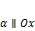 , когда
, когда 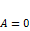 ;
;
· 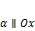 , когда
, когда 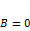 ;
;
· 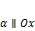 , когда
, когда 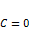 ;
;
· 
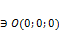 , когда
, когда 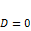 ;
;
· 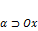 , когда
, когда 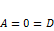 ;
;
· 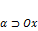 , когда
, когда 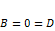 ;
;
· 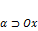 , когда
, когда 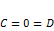 ;
;
· 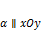 , когда
, когда 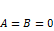 ;
;
· 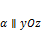 , когда
, когда 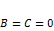 ;
;
· 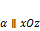 , когда
, когда 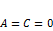 .
.
Взаимное расположение двух плоскостей в пространстве. Теоремы 1-3
Теорема. Пусть даны две плоскости: 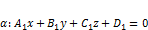 и
и 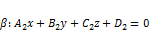 . Тогда:
. Тогда:
· 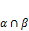 , когда
, когда 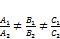 ;
;
· 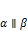 , когда
, когда 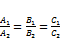 ;
;
·  , когда
, когда 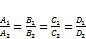 .
.
Уравнение прямой, проходящей через данную точку в заданном направлении. Параметрические уравнения прямой. Теорема
Теорема. Пусть прямая 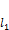 , коллинеарный ненулевому вектору
, коллинеарный ненулевому вектору 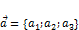 , проходит через
, проходит через 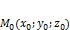 , тогда уравнение прямой проходящей через заданную точку и ненулевой вектор задаётся уравнением:
, тогда уравнение прямой проходящей через заданную точку и ненулевой вектор задаётся уравнением:
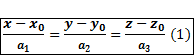
В параметрической форме:
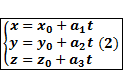
Доказательство:
· Произвольная точка 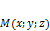 лежит на
лежит на 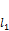 тогда и только тогда, когда
тогда и только тогда, когда 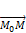 коллинеарен
коллинеарен  , что равносильно уравнению (1).
, что равносильно уравнению (1).
· Так как  – ненулевой, то
– ненулевой, то 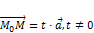 . Записав это уравнение в координатной форме, мы получаем (2).
. Записав это уравнение в координатной форме, мы получаем (2).
Уравнения прямой, проходящей через две заданные точки в пространстве. Теорема
Теорема. Пусть точки 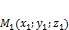 и
и 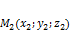 лежат на прямой
лежат на прямой 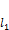 . Тогда прямая
. Тогда прямая 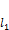 задаётся уравнением прямой, проходящей через две заданные точки:
задаётся уравнением прямой, проходящей через две заданные точки:
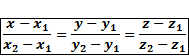
Доказательство:
1. Если за направляющий вектор 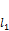 взять
взять 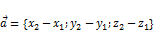 коллинеарный
коллинеарный 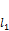 , то тогда в силу теоремы предыдущей темы прямая задаётся уравнением (1).
, то тогда в силу теоремы предыдущей темы прямая задаётся уравнением (1).
Взаимное расположение двух прямых в пространстве. Теоремы 1-4
Теоремы. Пусть относительно прямоугольно-декартовой системы координат в пространстве заданы две прямые своими уравнениями: 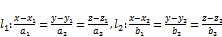 . Тогда
. Тогда
1. 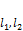 – скрещивающиеся, если
– скрещивающиеся, если 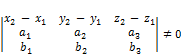 ;
;
2. 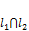 , если
, если 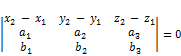 ;
;
3. 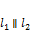 , если
, если 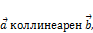 но
но 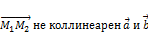 ;
;
4. 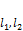 – совпадают если
– совпадают если 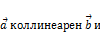
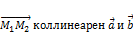 .
.
 2020-09-24
2020-09-24 162
162








