2020-10-09
401
Практическая часть
Пример 5.1. Имеются три урны. В первой урне 1 белый и 1 черный шар, во второй – 2 белых и 3 черных шара, в третьей – 4 белых и 7 черных шаров. Из выбранной наугад урны вынимают один шар. Найти вероятность того, что этот шар белый.
Решение. Пусть событие 
- извлечен белый шар.
Гипотезы:
- выбрана первая урна;
- выбрана вторая урна;
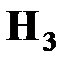- выбрана третья урна.
События 
, 
, 
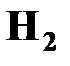- попарно несовместны и образуют полную группу.
Поскольку всего имеется три гипотезы, причем выбор любой из урн равновозможен, и сумма вероятностей гипотез равна единице (так как они образуют полную группу событий), то вероятность каждой из гипотез равна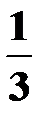 
, т. е.
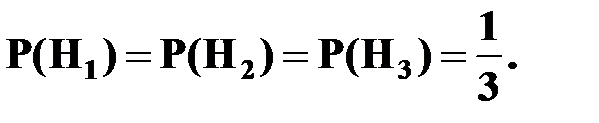
Вычислим условные вероятности:
- вероятность извлечения белого шара из первой урны;
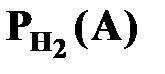- вероятность извлечения белого шара из второй урны;
- вероятность извлечения белого шара из третьей урны.
Вероятность события подсчитываем по формуле полной вероятности:
.
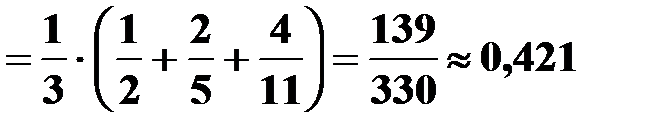Пример 5.2. В супермаркет однотипные товары поставляются тремя фирмами в отношении 1:3:5. Среди продукции первой фирмы качественные товары составляют 90%, второй – 80%, третьей - 95%. Приобретенный товар оказался некачественным. Найти вероятность того, что оно является продукцией первой фирмы.
Решение. Пусть событие - товар некачественный.
Гипотезы:
- товар является продукцией первой фирмы;
- товар является продукцией второй фирмы;
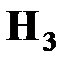- товар является продукцией третьей фирмы.
События , , 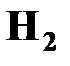- попарно несовместны и образуют полную группу.
Известно, что товары поставляются тремя фирмами в отношении 1:3:5. Пусть коэффициент пропорциональности 
. Тогда первая фирма поставляет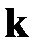 
товаров, вторая - 
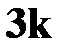, третья - 
.
Вероятность гипотез до появления события 
:
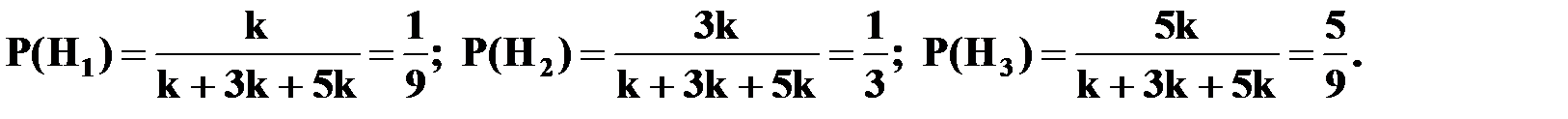
Условные вероятности:
- вероятность того, что продукция первой фирмы некачественная;
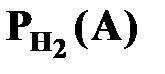- вероятность того, что продукция второй фирмы некачественная;
- вероятность того, что продукция третьей фирмы некачественная.
Вероятность события находим по формуле полной вероятности:
.
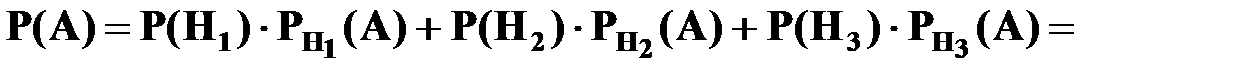
Искомая вероятность того, что приобретенный некачественный товар является продукцией первой фирмы, вычисляется по формуле Бейеса
.
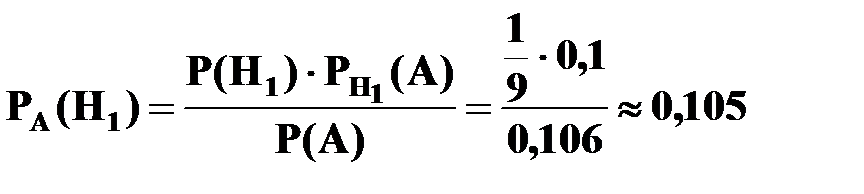Пример 5.3. Страховая компания разделяет застрахованных по трем классам риска: 1 класс – малый риск, 2 класс – средний, 3 класс – большой риск. Среди всех клиентов компании клиентов первого класса риска в два раза больше, чем второго, и в три раза больше, чем третьего. Вероятность наступления страхового случая для первого класса риска равна 0,01, второго – 0,03, третьего – 0,08. Какова вероятность того, что клиент, получивший денежное вознаграждение за период страхования, относится к группе среднего риска?
Решение. Пусть событие - клиент получил денежное вознаграждение за период страхования.
Гипотезы:
- клиент относится к группе малого риска;
- клиент относится к группе среднего риска;
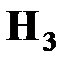- клиент относится к группе большого риска.
События , , 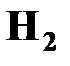- попарно несовместны и образуют полную группу.
Пусть вероятность того, что клиент компании относится к группе малого риска 
. Так как среди всех клиентов компании клиентов первого класса риска в два раза больше, чем второго и в три раза больше, чем третьего, то вероятности гипотез , , будут равны: 
Поскольку гипотезы образуют полную группу событий, то 
. Тогда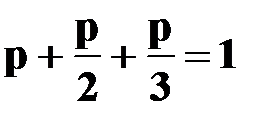 
. Следовательно, 
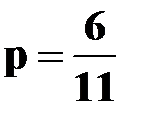. Таким образом,
Условные вероятности:
- вероятность получения страховки клиентом 1- го класса;
- вероятность получения страховки клиентом 2 - го класса;
- вероятность получения страховки клиентом 3 - го класса.
.
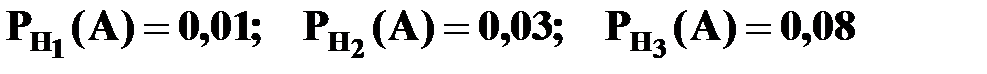Вероятность события подсчитываем по формуле полной вероятности:
.
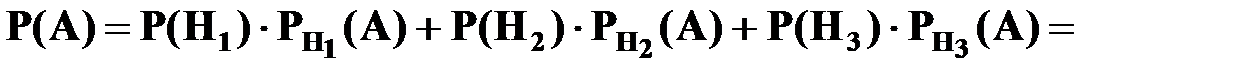
Искомая вероятность того, что клиент, получивший денежное вознаграждение за период страхования, относится к группе среднего риска, вычисляется по формуле Бейеса 
.
