первой промежуточной аттестации
1. 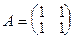 , , 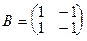 . Вычислить . Вычислить 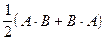 . .
| 2. В группе 25 студентов. Из них 5 человек получили на экзаменах отличные оценки, 12 — хорошие, 6 — удовлетворительные и 2 — неудовлетворительные. Определить вероятность того, что произвольно выбранный студент получил: 1) удовлетворительную оценку; 2) оценку не ниже хорошей. | ||||||||||
3. Вычислить предел: 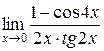
| 4. Вычислить предел: 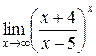 . .
| ||||||||||
5. Вычислить производную:
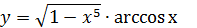
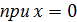
| 6. Вычислить производную:
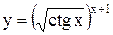
| ||||||||||
7. Найти значение интеграла:
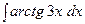
| 8. Найти значение интеграла:
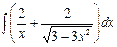
| ||||||||||
| 9.Два футболиста поражают ворота с 11 метров с вероятностями 0,9 и 0,95. Найти вероятность того, что только один мяч, после двух ударов, оказался в воротах. | 10.Дискретная случайная величина Х заданна законом распределения:
Найти математическое ожидание М(Х) и дисперсию D(Х) и среднее квадратическое отклонение |
Экзаменационный билет №109
первой промежуточной аттестации
| 1.В телевизионном ателье имеются 4 кинескопа. Вероятности того, что кинескоп выдержит гарантийный срок службы, соответственно равны 0,8; 0,85; 0,9; 0,95. Найти вероятность того, что взятый наудачу кинескоп выдержит гарантийный срок службы. | 2. Решить систему методом Гаусса:
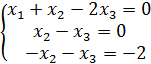
| ||||||||
3. Вычислить предел:
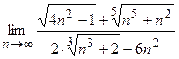
| 4. Вычислить предел:
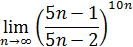
| ||||||||
5. Найти производную 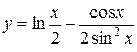
| 6. Найти производную 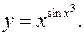
| ||||||||
7. Найти значение интеграла: 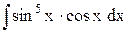
| 8. Найти значение интеграла: 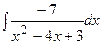
| ||||||||
| 9.В урне 4 белых и 6 черных шаров. Из урны вынимается один шар, отмечается его цвет и шар возвращается в урну. После этого из урны берется еще один шар. Найти вероятность того, что оба вынутых шара одного цвета. | 10.Дискретная случайная величина Х заданна законом распределения:
Найти среднеквадратическое отклонение этой величины. |
 2020-10-10
2020-10-10 253
253

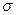 (Х) случайной величины.
(Х) случайной величины.






