первой промежуточной аттестации
| 1. Из 10 деталей 4 окрашены. Вероятность того, что окрашенная деталь тяжелее нормы, равна 0,3, а для неокрашенной детали эта вероятность равна 0,1. Взятая наудачу деталь оказалась легче нормы. Найти вероятность того, что она окрашена. | 2. Найти 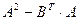 , если , если  , , 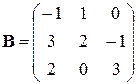
| ||||||||
3. Вычислить предел:
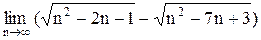
| 4. Вычислить предел:
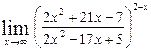
| ||||||||
5. Вычислить производную:
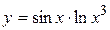
| 6. Найти производную 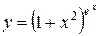
| ||||||||
7. Найти значение интеграла:
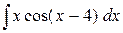
| 8. Найти значение интеграла:
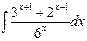
| ||||||||
| 9. В двух урнах находятся шары, отличающиеся только цветом, причем в первой урне 4 белых, 5 черных и 1 красный, а во второй урне — 3, 5, 2 соответственно. Из обеих урн наудачу извлекается по одному шару. Какова вероятность того, что оба шара одного цвета? | 10.Дискретная случайная величина Х заданна законом распределения:
Найти среднее квадратическое отклонение этой величины |
Экзаменационный билет №105
первой промежуточной аттестации
| 1. В группе спортсменов 5 лыжников, 6 велосипедистов и 4 бегуна. Вероятность выполнить квалификационную норму равна: для лыжника – 0,9, для велосипедиста – 0,8 и для бегуна – 0,75. Найти вероятность того, что спортсмен выбранный наудачу, выполнит норму. | 2. Найти  , если , если 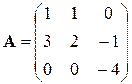 , , 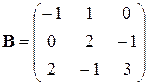
| ||||||||||
3. Вычислить предел: 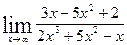
| 4. Вычислить предел:
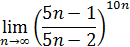
| ||||||||||
5. Вычислить производную:
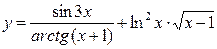
| 6. Вычислить производную:

| ||||||||||
7. Найти значение интеграла: 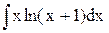
| 8. Найти значение интеграла: 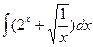
| ||||||||||
| 9.Изделия некоторого производства содержат 5% брака. Найти вероятность того, что среди пяти взятых наудачу изделий окажется 3 бракованных изделия. | 10.Дискретная случайная величина Х заданна законом распределения:
Найти дисперсию D(Х) и среднее квадратическое отклонение |
 2020-10-10
2020-10-10 231
231

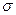 (Х) случайной величины.
(Х) случайной величины.






