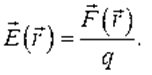| Электрическое поле, созданное неподвижным зарядом (или системой неподвижных зарядов), называется электростатическим. |
Посредством электростатического поля осуществляется взаимодействие между зарядами. Само понятие поля оказалось весьма плодотворным и широко используется в современной физике. Появление поля означает, что что-то изменилось в окружающем нас пространстве. Математически поле описывается величиной, меняющейся от точки к точке. Например, можно рассмотреть поле скоростей в текущей жидкости. В каждой точке объема жидкости задан вектор скорости, который может меняться со временем (нестационарное течение), а может и быть постоянным (стационарное течение). Это пример векторного поля. К этому же типу полей относится и поле неподвижных электрических зарядов.
Напишем выражение для силы, действующей на точечный заряд 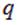 в результате его взаимодействия с системой точечных зарядов
в результате его взаимодействия с системой точечных зарядов 
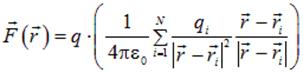
| (1.6) |
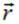 — радиус-вектор точки, в которой находится заряд
— радиус-вектор точки, в которой находится заряд 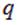 . Заряд
. Заряд 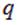 , на который, действует сила, в подобных ситуациях иногда называют «пробным» зарядом, выписан отдельным множителем. Выражение, стоящее в круглых скобках, определяется исключительно свойствами той системы зарядов, которая воздействует на заряд
, на который, действует сила, в подобных ситуациях иногда называют «пробным» зарядом, выписан отдельным множителем. Выражение, стоящее в круглых скобках, определяется исключительно свойствами той системы зарядов, которая воздействует на заряд 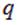 . Естественно, что это воздействие (сила) зависит от того, где он находится, соответственно, выражение в круглых скобках зависит от радиус-вектора
. Естественно, что это воздействие (сила) зависит от того, где он находится, соответственно, выражение в круглых скобках зависит от радиус-вектора 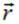 , определяющего местоположение заряда
, определяющего местоположение заряда 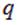 . Следуя изложенной выше идее об электростатическом поле существующем вокруг каждого заряда и, разумеется, системы зарядов, введем силовую характеристику этого поля, называемую напряженностью электрического поля.
. Следуя изложенной выше идее об электростатическом поле существующем вокруг каждого заряда и, разумеется, системы зарядов, введем силовую характеристику этого поля, называемую напряженностью электрического поля.
Напряженностью электрического поля называется вектор  , равный отношению силы, действующей на точечный заряд , равный отношению силы, действующей на точечный заряд 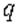 к алгебраической величине этого заряда (рис. 1.12) к алгебраической величине этого заряда (рис. 1.12)
|
Напряженность поля точечного заряда в различных точках пространства, в общем случае различна и по величине и по направлению (рис. 1.14). Поле точечного заряда — центральное поле, центр симметрии поля совпадает с точкой, в которой находится заряд.
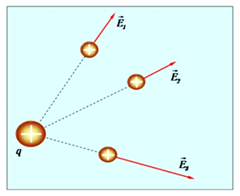
Рис. 1.14. Векторы напряженности электрического поля заряда q в разных точках пространства
В СИ единицей измерения напряженности электрического поля является ньютон на кулон (Н/Кл), — то есть за единицу напряженности поля принята напряженность такого поля, в котором на заряд равный 1 Кл действует сила, равная 1 Н:
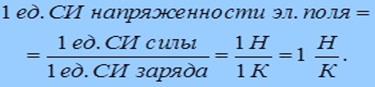
|
Электрическое поле можно задать, указав для каждой точки величину и направление вектора напряженности электрического поля 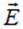 . Для наглядного изображения электрического поля используют силовые линии (или линии векторного поля
. Для наглядного изображения электрического поля используют силовые линии (или линии векторного поля 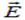 ).
).
| Линией напряженности электрического поля (силовой линией) называется такая линия, касательная к которой в каждой её точке совпадает по направлению с вектором напряженности электрического поля. |

На рис. 1.17 показана силовая линия электрического поля. Векторы напряженности электрического поля направлены по касательной к силовой линии.
Рис. 1.17. Векторы напряженности электрического поля направлены по касательной к силовым линиям
Отметим некоторые важные свойства силовых линий электростатического поля:
- силовые линии начинаются на положительных зарядах (или на бесконечности) и заканчиваются на отрицательных зарядах (или на бесконечности);
силовые линии нигде не пересекаются (в противном случае, напряжённость поля 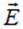 была бы неоднозначной функцией координат точки);
была бы неоднозначной функцией координат точки);
В разделе «Механика» было показано, что консервативная сила 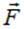 связана с потенциальной энергией
связана с потенциальной энергией 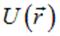 соотношением
соотношением
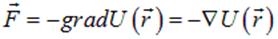
| (1.11) |
Здесь знак 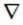 — общепринятое обозначение векторного оператора «набла», результат действия которого на скалярную функцию координат есть градиент этой функции. Явный вид оператора набла в декартовых координатах следующий:
— общепринятое обозначение векторного оператора «набла», результат действия которого на скалярную функцию координат есть градиент этой функции. Явный вид оператора набла в декартовых координатах следующий:
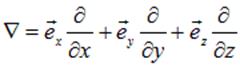
| (1.12) |
Подставив в 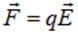 и разделив на
и разделив на 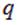 , получаем
, получаем
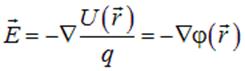
| (1.13) |
Скалярная функция 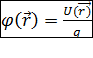 называется потенциалом электрического поля.
называется потенциалом электрического поля.
Функция 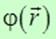 , связанная с напряженностью электростатического поля соотношением , связанная с напряженностью электростатического поля соотношением
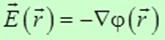 ,
называется потенциалом электростатического поля. ,
называется потенциалом электростатического поля.
|
Как видно из (1.13), потенциальная энергия точечного заряда 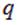 в поле с потенциалом
в поле с потенциалом 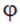 равна
равна
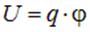
| (1.14) |
а действующая на него сила 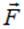
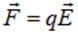
| (1.15) |
В СИ единицей измерения потенциала электрического поля является вольт(В):
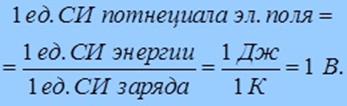
|
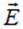 Напряженность поля определяет силу, действующую в поле на точечный заряд, а потенциал — его потенциальную энергию в этом поле. Поэтому, следуя смыслу соотношений и, напряженность электрического поля называют силовой характеристикой поля, а потенциал
Напряженность поля определяет силу, действующую в поле на точечный заряд, а потенциал — его потенциальную энергию в этом поле. Поэтому, следуя смыслу соотношений и, напряженность электрического поля называют силовой характеристикой поля, а потенциал 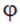 — его энергетической характеристикой.
— его энергетической характеристикой.
Как и потенциальная энергия, потенциал поля всегда определен с точностью до аддитивной постоянной. Это видно из: поскольку набла есть дифференциальный оператор, потенциалы 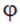 и
и 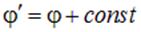 физически тождественны, так как им соответствует поле одной и той же напряженности
физически тождественны, так как им соответствует поле одной и той же напряженности
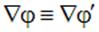 .
.
Это позволяет нормировать потенциал, произвольно выбирая некоторую точку 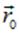 и полагая потенциал в этой точке равным нулю
и полагая потенциал в этой точке равным нулю
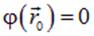
| (1.16) |
Учитывая, что и напряженность поля, и потенциал поля убывают с ростом расстояния 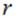 до системы зарядов, создающей поле, во всех тех случаях, когда конечный
до системы зарядов, создающей поле, во всех тех случаях, когда конечный 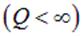 заряд распределен по конечной области пространства, нормировать потенциал естественно и удобно на «нуль на бесконечности», то есть полагать его равным нулю на бесконечном удалении от системы зарядов
заряд распределен по конечной области пространства, нормировать потенциал естественно и удобно на «нуль на бесконечности», то есть полагать его равным нулю на бесконечном удалении от системы зарядов
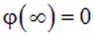
| (1.17) |
Соотношение (1.13) позволяет вычислить напряженность поля по известному потенциалу;
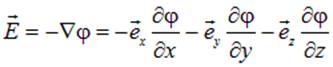
| (1.18) |
Получим «обратную» связь: выразим потенциал поля через его напряженность. Для этого сравним три выражения: выражение для 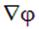 из (1.18), выражение для вектора бесконечно малого перемещения
из (1.18), выражение для вектора бесконечно малого перемещения 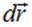 и выражение для полного дифференциала
и выражение для полного дифференциала 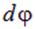 функции
функции 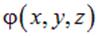 :
:
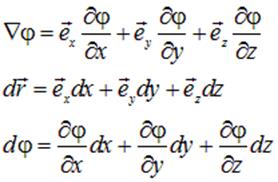
Нетрудно видеть, что скалярное произведение двух первых векторов равно полному дифференциалу 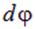 потенциала
потенциала
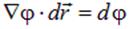
| (1.19) |
или, с учетом
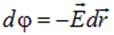
| (1.20) |
На самом деле это соотношение не новое. Если умножить (1.20) на заряд 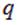 и учесть связи (1.14) и (1.15), мы получим знакомое по разделу «Механика» соотношение, связывающее работу консервативной силы и убыль потенциальной энергии
и учесть связи (1.14) и (1.15), мы получим знакомое по разделу «Механика» соотношение, связывающее работу консервативной силы и убыль потенциальной энергии
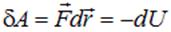 .
.
Там же, в разделе «Механика» было показано, что стационарное потенциальное поле консервативно. Из соотношения (1.18) вытекает, что электростатическое поле консервативно во всех тех случаях, когда потенциал поля не зависит от времени.
Интегрируя соотношение (1.20) от точки 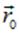 , потенциал в которой принят равным нулю, до некоторой точки
, потенциал в которой принят равным нулю, до некоторой точки 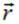 , потенциал в которой нас интересует, вдоль произвольной, удобной для вычислений кривой (поле консервативно и от формы кривой результат не зависти), получаем
, потенциал в которой нас интересует, вдоль произвольной, удобной для вычислений кривой (поле консервативно и от формы кривой результат не зависти), получаем
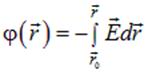
| (1.21) |
Вычислим с помощью (1.21) потенциал поля точечного заряда 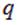 , находящегося в начале координат, нормировав его на нуль на бесконечном удалении от этого заряда. Воспользуемся для этого законом Кулона в форме (1.9):
, находящегося в начале координат, нормировав его на нуль на бесконечном удалении от этого заряда. Воспользуемся для этого законом Кулона в форме (1.9):
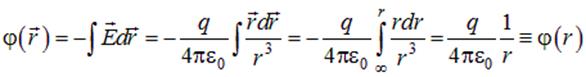
| (1.22) |
При вычислении использовано тождество 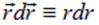 , справедливое для любого вектора
, справедливое для любого вектора 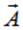 :
: 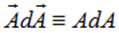 и являющееся результатом простого дифференцирования определения модуля любого вектора:
и являющееся результатом простого дифференцирования определения модуля любого вектора: 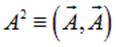 .
.
Таким образом, потенциал поля точечного заряда находящегося в начале координат имеет вид
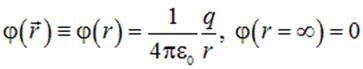
| (1.23) |
и поле это, как уже отмечалось ранее, центральное: фактически потенциал поля зависит только от 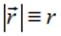 .
.
Учитывая, что стоящий в знаменателе модуль радиус-вектора 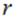 есть ни что иное как расстояние от заряда, создающего поле до точки наблюдения поля, формулу легко обобщить на случай, когда заряд
есть ни что иное как расстояние от заряда, создающего поле до точки наблюдения поля, формулу легко обобщить на случай, когда заряд 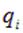 находится не в начале координат, а в точке с радиус-вектором
находится не в начале координат, а в точке с радиус-вектором 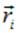 . В этом случае расстояние от заряда до точки наблюдения поля равно
. В этом случае расстояние от заряда до точки наблюдения поля равно 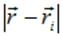 и потенциал поля в точке
и потенциал поля в точке 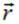 (при прежней нормировке на нуль на бесконечности) равен
(при прежней нормировке на нуль на бесконечности) равен

| (1.24) |
Связь между напряженностью поля и его потенциалом  линейная, поэтому принцип суперпозиции для напряженности поля справедлив и для потенциала поля. Другими словами: потенциал поля системы зарядов равен алгебраической сумме потенциалов поля от каждого из зарядов системы. Используя принцип суперпозиции, потенциал поля системы зарядов можно написать сразу
линейная, поэтому принцип суперпозиции для напряженности поля справедлив и для потенциала поля. Другими словами: потенциал поля системы зарядов равен алгебраической сумме потенциалов поля от каждого из зарядов системы. Используя принцип суперпозиции, потенциал поля системы зарядов можно написать сразу 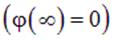 :
:
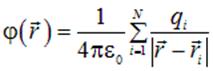
| (1.25) |
Здесь 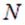 — полное число зарядов в системе.
— полное число зарядов в системе.
В случае непрерывного распределения заряда по некоторому объему 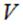 , получим
, получим
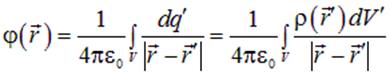
| (1.26) |
При непрерывном распределении заряда по некоторой поверхности 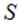 или кривой
или кривой 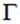 , получим соответственно
, получим соответственно
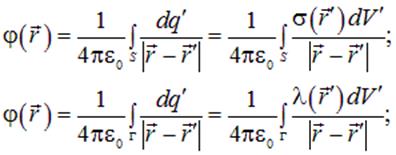
| (1.27) |
где 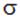 и
и 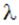 — соответствующие поверхностная и линейная плотности.
— соответствующие поверхностная и линейная плотности.
В Дополнении 4 разобран пример использования только что полученных соотношений.
Мы не будем рассматривать здесь отдельно вопрос о работе электростатических сил при перемещении в электростатическом поле точечных зарядов и заряженных тел. Электростатическое поле консервативно (рис. 1.26), потенциальная энергия заряда в поле равна 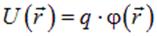 , поэтому работа электростатических сил всегда может быть вычислена с помощью соотношений вида
, поэтому работа электростатических сил всегда может быть вычислена с помощью соотношений вида
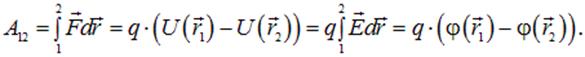
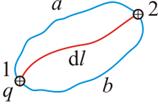
Рис. 1.26. Работа электростатических сил зависит только от положения начальной и конечной точек
Вычислим энергию взаимодействия зарядов, входящих с состав некоторой системы.
Для нумерации этих зарядов удобно использовать два индекса, например, 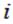 и
и 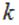 . Одни и те же заряды системы, один раз это
. Одни и те же заряды системы, один раз это 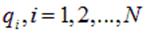 , другой раз это
, другой раз это 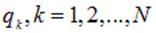 . Подчеркнем, что заряд
. Подчеркнем, что заряд 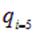 и заряд
и заряд 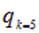 это один и тот же 5-ый заряд системы. Такие «сложности» необходимы для компактной записи выражения для их энергии взаимодействия и вот почему. Заряды взаимодействуют попарно, энергия взаимодействия
это один и тот же 5-ый заряд системы. Такие «сложности» необходимы для компактной записи выражения для их энергии взаимодействия и вот почему. Заряды взаимодействуют попарно, энергия взаимодействия 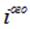 и
и 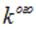 зарядов согласно равна
зарядов согласно равна
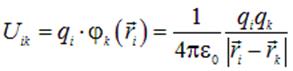
| (1.28) |
Здесь 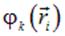 — потенциал
— потенциал 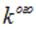 заряда в той точке, где находится
заряда в той точке, где находится 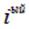 заряд.
заряд.
Для наглядного представления распределения потенциала в пространстве используются эквипотенциальные поверхности.
| Эквипотенциальная поверхность (поверхность равного потенциала) — это совокупность точек, имеющих равный потенциал. |
Мы хотим подчеркнуть, что при решении макроскопических задач, в подавляющем большинстве случаев, можно считать, что заряд распределён непрерывно, соответственно, вычислять надо не суммы, а интегралы. Поэтому встает задача: на базе закона Кулона и принципа суперпозиции, написать интегральные и/или дифференциальные уравнения, которым удовлетворяет напряженность поля произвольного распределения зарядов. Эту задачу в ряде случаев успешно решает обсуждаемая в этом параграфе теорема Гаусса для вектора 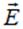 .
.
Рассмотрим некоторую поверхность 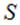 и на ней бесконечно малый участок (бесконечно малую площадку) площадью
и на ней бесконечно малый участок (бесконечно малую площадку) площадью 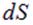 (рис. 1.34).
(рис. 1.34).
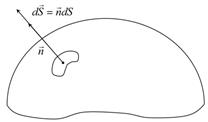
Рис. 1.34. Бесконечно малый участок поверхности
Показанный на рисунке «вектор площадки» 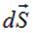 имеет следующий смысл: 1) он направлен по нормали
имеет следующий смысл: 1) он направлен по нормали 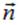 к поверхности
к поверхности 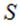 в той её точке, в окрестности которой находится площадка; 2) его модуль равен площади площадки
в той её точке, в окрестности которой находится площадка; 2) его модуль равен площади площадки 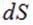 . Вектор
. Вектор 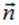 , а вместе с ним и вектор
, а вместе с ним и вектор 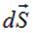 всегда направлены по перпендикуляру к поверхности в данном её месте, а вот в какую сторону: налево вверх, как на рисунке выше, или в противоположную сторону (направо вниз, «под» поверхность), — в общем случае это дело произвольного выбора. Однако в ряде случаев, по умолчанию, действуют определенные правила. Например, если поверхность замкнутая, то есть представляет собой некоторую замкнутую «оболочку», то по умолчанию берется «внешняя» нормаль, направленная наружу. Выбор «внутренней» нормали ничему не противоречит, но должен быть специально оговорен. Если поверхность не замкнутая и опирается на некоторый контур, а, кроме того, задано направление обхода этого контура, то направление нормали общепринято связывать с направлением обхода правилом правого винта. С той же оговоркой, что и выше: направление обхода контура и направление нормали к поверхности, которая на него опирается, можно связать, используя левый, а не правый винт, такой выбор ничему не противоречит, но должен быть специально оговорен. Здесь и ниже, если иное специально не оговорено, будут использоваться указанные выше общепринятые правила: внешняя нормаль и правый винт.
всегда направлены по перпендикуляру к поверхности в данном её месте, а вот в какую сторону: налево вверх, как на рисунке выше, или в противоположную сторону (направо вниз, «под» поверхность), — в общем случае это дело произвольного выбора. Однако в ряде случаев, по умолчанию, действуют определенные правила. Например, если поверхность замкнутая, то есть представляет собой некоторую замкнутую «оболочку», то по умолчанию берется «внешняя» нормаль, направленная наружу. Выбор «внутренней» нормали ничему не противоречит, но должен быть специально оговорен. Если поверхность не замкнутая и опирается на некоторый контур, а, кроме того, задано направление обхода этого контура, то направление нормали общепринято связывать с направлением обхода правилом правого винта. С той же оговоркой, что и выше: направление обхода контура и направление нормали к поверхности, которая на него опирается, можно связать, используя левый, а не правый винт, такой выбор ничему не противоречит, но должен быть специально оговорен. Здесь и ниже, если иное специально не оговорено, будут использоваться указанные выше общепринятые правила: внешняя нормаль и правый винт.
Введём в рассмотрение поток 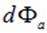 произвольного вектора
произвольного вектора 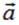 через выбранную площадку. По определению:
через выбранную площадку. По определению:
Поток 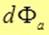 вектора вектора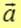 через бесконечно малую площадку через бесконечно малую площадку 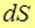 есть скалярное произведение вектора есть скалярное произведение вектора 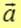 на вектор площадки на вектор площадки 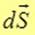 : :
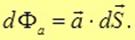
|
Формально рассматривается бесконечно малая площадка, фактически (например, при численном суммировании) она должна быть настолько мала, чтобы в её пределах вектор 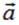 можно было считать неизменным (однородным), а саму площадку плоской, тогда не возникает проблемы, в какой точке внутри площадки проводить нормаль к ней.
можно было считать неизменным (однородным), а саму площадку плоской, тогда не возникает проблемы, в какой точке внутри площадки проводить нормаль к ней.
Для общности определения (в физике рассматриваются потоки и других векторов) выше был рассмотрен произвольный вектор 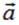 , применительно к вектору напряженности электрического поля
, применительно к вектору напряженности электрического поля 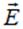 , с учетом замечания о размерах площадки, определение потока иллюстрирует рис. 1.35.
, с учетом замечания о размерах площадки, определение потока иллюстрирует рис. 1.35.
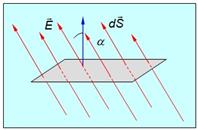
Рис. 1.35. Поток вектора напряженности электрического поля через бесконечно малую площадку
Согласно определению, поток вектора напряженности через площадку равен (здесь и в дальнейшем, для краткости, когда это будет удобным, будем писать: «площадка» и указывать при этом вектор этой площадки, которым полностью определены и её площадь и ориентация):
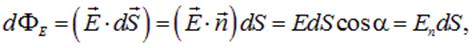
| (1.43) |
где α — угол между векторами 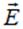 и
и 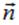 ,
, 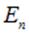 — нормальная к поверхности составляющая вектора
— нормальная к поверхности составляющая вектора 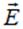 . Подчеркнем, что изменение направления нормали
. Подчеркнем, что изменение направления нормали 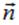 как и изменение направления вектора напряженности на обратное меняет знак потока на противоположный, таким образом, поток вектора - величина алгебраическая.
как и изменение направления вектора напряженности на обратное меняет знак потока на противоположный, таким образом, поток вектора - величина алгебраическая.
Поток вектора 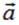 через произвольную поверхность S равен сумме потоков через все площадки, на которые разбита поверхность S, то есть интегралу по этой поверхности вида:
через произвольную поверхность S равен сумме потоков через все площадки, на которые разбита поверхность S, то есть интегралу по этой поверхности вида:
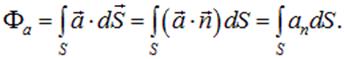
| (1.32) |
Если векторное поле 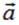 однородно, то есть
однородно, то есть 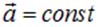 , а поверхность плоская, то
, а поверхность плоская, то
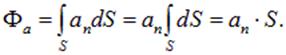
Здесь S — площадь этой поверхности. Для обозначения интеграла по замкнутой поверхности используется специальный значок интеграла, а именно: с кружком в середине (S — замкнутая поверхность) (рис. 1.36):
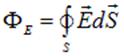
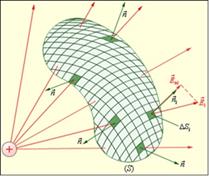
Рис. 1.36. Поток вектора напряженности электрического поля через замкнутую поверхность
Для уяснения смысла такой величины как поток вектора весьма полезно, в силу наглядности, рассмотрение потока жидкости, например, в реке или в трубе.
Теорема Гаусса для вектора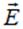 позволяет связать поток вектора напряженности через некоторую замкнутую поверхность с величиной зарядов, находящихся внутри этой поверхности. Рассмотрим для начала частный случай, а именно: определим поток вектора напряженности через произвольную воображаемую сферическую поверхность, в центре которой расположен точечный заряд. Линии напряжённости векторного поля
позволяет связать поток вектора напряженности через некоторую замкнутую поверхность с величиной зарядов, находящихся внутри этой поверхности. Рассмотрим для начала частный случай, а именно: определим поток вектора напряженности через произвольную воображаемую сферическую поверхность, в центре которой расположен точечный заряд. Линии напряжённости векторного поля 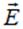 точечного заряда представляют собой радиальные прямые, направленные от заряда, если он положителен, и к заряду, если он отрицателен (см. рис. 1.12). Поток вектора напряженности поля точечного заряда через сферическую поверхность радиусом r, центр которой совпадает с положением заряда и началом координат, равен
точечного заряда представляют собой радиальные прямые, направленные от заряда, если он положителен, и к заряду, если он отрицателен (см. рис. 1.12). Поток вектора напряженности поля точечного заряда через сферическую поверхность радиусом r, центр которой совпадает с положением заряда и началом координат, равен
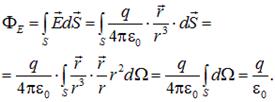
| (1.33) |
Здесь 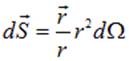 , где
, где 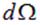 — элемент телесного угла, мы воспользовались значением полного телесного угла
— элемент телесного угла, мы воспользовались значением полного телесного угла
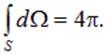
Можно показать, что поток вектора напряженности через любую замкнутую поверхность, охватывающую заряд q, не зависит от формы поверхности и равен 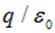 так же, как и для сферы. Физический смысл этого утверждения опять-таки заключается в том, что силовые линии начинаются и кончаются на зарядах. Поэтому непрерывная (без разрывов) деформация поверхности (показана на рис. 1.39-1 пунктиром) не изменит полного числа линий напряженности, выходящих наружу. Как следствие, поток через произвольную поверхность, охватывающую заряд, будет таким же, как и для сферы (см. рис. 1.39-1).
так же, как и для сферы. Физический смысл этого утверждения опять-таки заключается в том, что силовые линии начинаются и кончаются на зарядах. Поэтому непрерывная (без разрывов) деформация поверхности (показана на рис. 1.39-1 пунктиром) не изменит полного числа линий напряженности, выходящих наружу. Как следствие, поток через произвольную поверхность, охватывающую заряд, будет таким же, как и для сферы (см. рис. 1.39-1).
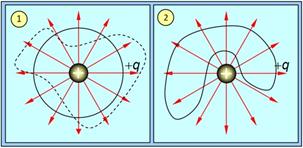
Рис. 1.39. Поток вектора Е через замкнутую поверхность:
1 — заряд находится внутри поверхности; 2 — заряд находится вне поверхности
Если же заряд находится вне ограниченного замкнутой поверхностью пространства, то линии напряжённости пронизывают поверхность чётное число раз (снаружи внутрь и изнутри наружу), в результате полный поток через поверхность, не охватывающую заряд, равен нулю (рис. 1.39-2).
Вывод теоремы Гаусса для точечного заряда, расположенного в произвольной точке, приведен в Дополнении 5.
Пусть теперь внутри и вне данной замкнутой поверхности имеется произвольное число точечных зарядов любого знака. В силу принципа суперпозиции суммарная напряженность поля будет представлять собой векторную сумму напряженностей полей каждого из зарядов
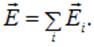
Полный поток напряженности поля через эту поверхность есть
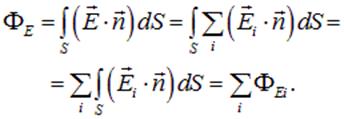
Используя, получаем соотношение, известное как теорема Гаусса для вектора 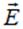 :
:
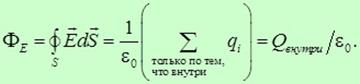
Поток вектора напряженности электрического поля через замкнутую поверхность равен полному зарядувнутриэтой поверхности делённому на 
|
Подчеркнем еще раз тривиальное, но важное обстоятельство: если внутри поверхности нет зарядов, то поток вектора 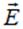 через эту поверхность равен нулю (рис. 1.40). Источниками электростатического поля являются электрические заряды и суммарная мощность источников электростатического поля внутри поверхности равна
через эту поверхность равен нулю (рис. 1.40). Источниками электростатического поля являются электрические заряды и суммарная мощность источников электростатического поля внутри поверхности равна 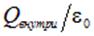 . Присутствие в последней формуле электрической постоянной
. Присутствие в последней формуле электрической постоянной 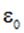 есть результат выбора системы единиц (СИ) и физического смысла не имеет.
есть результат выбора системы единиц (СИ) и физического смысла не имеет.

Рис. 1.40. Если внутри поверхности нет зарядов, то поток вектора 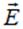 через эту поверхность равен нулю
через эту поверхность равен нулю
При непрерывном распределении заряда по объёму теорему Гаусса естественно записать в следующем виде
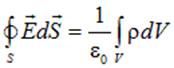
| (1.35) |
В правой части этого соотношения интеграл берется по объёму 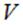 ограниченному поверхностью
ограниченному поверхностью 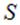 , поток
, поток 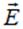 через которую вычисляется в левой его части. При непрерывном распределении заряда по некоторой поверхности справа будет стоять интеграл вида
через которую вычисляется в левой его части. При непрерывном распределении заряда по некоторой поверхности справа будет стоять интеграл вида 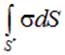 только по той части
только по той части 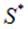 несущей заряд поверхности, которая оказалась внутри поверхности
несущей заряд поверхности, которая оказалась внутри поверхности 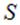 , стоящей слева. При непрерывном распределении заряда вдоль некоторой линии
, стоящей слева. При непрерывном распределении заряда вдоль некоторой линии 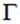 справа будет стоять интеграл вида
справа будет стоять интеграл вида 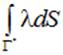 также только по той части
также только по той части 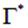 несущей заряд линии, которая оказалась внутри поверхности
несущей заряд линии, которая оказалась внутри поверхности 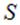 . Короче, необходимо любым приемлемым способом вычислить заряд внутри той замкнутой поверхности, по которой вычисляется поток вектора напряженности электрического поля. Теорема Гаусса для вектора
. Короче, необходимо любым приемлемым способом вычислить заряд внутри той замкнутой поверхности, по которой вычисляется поток вектора напряженности электрического поля. Теорема Гаусса для вектора 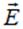
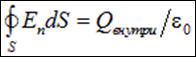
может быть успешно использована как эффективный инструмент расчета напряженности и потенциала электрического поля некоторого распределения заряда, когда стоящий слева интеграл может быть превращен в произведение площади поверхности, по которой производится интегрирование, на величину нормальной к поверхности составляющей вектора.
Вполне очевидно, что для расчета будет достаточно, во-первых, когда вектор 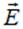 перпендикулярен поверхности. Следовательно, поверхность интегрирования должна быть эквипотенциальной поверхностью рассчитываемого поля. Её форму надо знать заранее. Наконец, во-вторых, во всех точках этой — эквипотенциальной — поверхности нормальная к ней составляющая
перпендикулярен поверхности. Следовательно, поверхность интегрирования должна быть эквипотенциальной поверхностью рассчитываемого поля. Её форму надо знать заранее. Наконец, во-вторых, во всех точках этой — эквипотенциальной — поверхности нормальная к ней составляющая 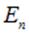 должна иметь одну и ту же величину, в противном случае, её нельзя будет вынести из-под знака интеграла и будет возможно найти лишь среднее на эквипотенциальной поверхности значение
должна иметь одну и ту же величину, в противном случае, её нельзя будет вынести из-под знака интеграла и будет возможно найти лишь среднее на эквипотенциальной поверхности значение 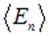 . Подчеркнем, что из факта эквипотенциальности поверхности, а именно, из того, что
. Подчеркнем, что из факта эквипотенциальности поверхности, а именно, из того, что
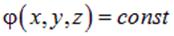
вовсе не вытекает, что и
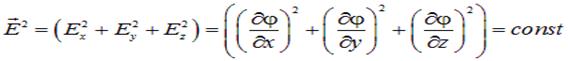
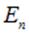 в точках этой поверхности. Забегая вперед, укажем, что, например, поверхность заряженного проводника при условии равновесного распределения заряда на нем всегда эквипотенциальна, но, если это не шар, а тело сложной формы, то в окрестности выступов (острий) напряженность поля может быть на порядки больше, чем в окрестности впадин на поверхности. Требование постоянства — отдельное требование.
в точках этой поверхности. Забегая вперед, укажем, что, например, поверхность заряженного проводника при условии равновесного распределения заряда на нем всегда эквипотенциальна, но, если это не шар, а тело сложной формы, то в окрестности выступов (острий) напряженность поля может быть на порядки больше, чем в окрестности впадин на поверхности. Требование постоянства — отдельное требование.
Из сказанного выше вытекает, что теорема Гаусса в состоянии быстро и просто привести к результату (вектору 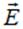 ) лишь в том случае, когда создающее поле распределение заряда обладает высокой степенью симметрии, соответственно, заранее известна форма эквипотенциальных поверхностей поля и есть уверенность в том, что
) лишь в том случае, когда создающее поле распределение заряда обладает высокой степенью симметрии, соответственно, заранее известна форма эквипотенциальных поверхностей поля и есть уверенность в том, что 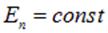 на этих поверхностях. Если всё это имеет место, то решение выглядит следующим простым образом:
на этих поверхностях. Если всё это имеет место, то решение выглядит следующим простым образом:
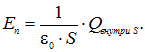
| (1.36) |
Остается выбрать поверхность 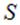 согласно симметрии распределения заряда и вычислить заряд внутри
согласно симметрии распределения заряда и вычислить заряд внутри  .
.
 2020-10-10
2020-10-10 676
676