Среди всех чисел, ограничивающих сверху и снизу данное множество, наименьшее и наибольшее из них имеют специальные названия.
Определение 1. Наибольшее из всех чисел, ограничивающих снизу подмножество  ℝ, называется его нижней гранью:
ℝ, называется его нижней гранью: 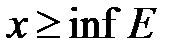 . (inf от латинского слова инфимум – «наименьший», «наинизший»).
. (inf от латинского слова инфимум – «наименьший», «наинизший»).
Обозначение: 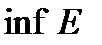 или
или 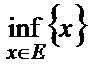 .
.
Пример. Дано ограниченное снизу множество  ,
, 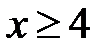 ,
, 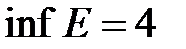 .
.
Множество  ограничивают снизу и такие числа
ограничивают снизу и такие числа 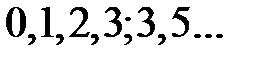 .
.
Но из них число  наибольшее.
наибольшее.  .
.
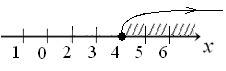
А из элементов множества 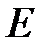 число
число 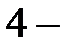 самое наименьшее.
самое наименьшее.  ,
,  . Поэтому в переводе «inf» – наименьший, наинизший.
. Поэтому в переводе «inf» – наименьший, наинизший.
Определение 2. Наименьшее из всех чисел, ограничивающих сверху множество  ℝ, называется его верхней гранью:
ℝ, называется его верхней гранью: 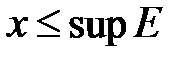 . (sup – латинского слова супремум – в переводе наибольший, наивысший)
. (sup – латинского слова супремум – в переводе наибольший, наивысший)
Обозначение:  или
или 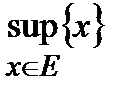 .
.
Пример 1. Дано множество 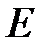 , ограниченное сверху.
, ограниченное сверху. 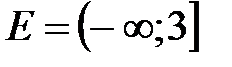 ,
, 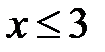 .
.
Множество 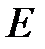 ограничивают сверху и такие числа: 4, 5, 6… Но число
ограничивают сверху и такие числа: 4, 5, 6… Но число  наименьшее из всех чисел, ограничивающих сверху множество
наименьшее из всех чисел, ограничивающих сверху множество 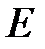 .
.
А из элементов множества 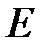 число
число 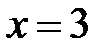 – самое наибольшее, наивысшее.
– самое наибольшее, наивысшее.
sup 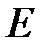 =3
=3 
Пример 2. Пусть множество действительных чисел  есть интервал
есть интервал 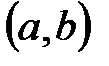 , т.е.
, т.е.  , тогда
, тогда  .
.
Определение 3. Верхнюю и нижнюю грани множества называют точной верхней и точной нижней гранями (границами) множества.
Замечание. Если множество 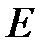 не ограниченно сверху, то пишут
не ограниченно сверху, то пишут  .
.
Если множество 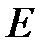 не ограниченно снизу, то пишут
не ограниченно снизу, то пишут 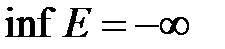 .
.
 2020-10-10
2020-10-10 289
289








