Лекция №3
1. Лемма о непересекающихся окрестностях.
2. Ограниченные и неограниченные множества.
3. Верхняя и нижняя грани числовых множеств.
4. Свойства точных граней множества.
5. Плотность множества рациональных чисел во множестве действительных чисел.
Лемма
Лемма – греческое слово (вспомогательное утверждение, необходимое в цепи логических рассуждений для доказательства некоторой теоремы).
Лемма. Пусть  ℝ, причем
ℝ, причем 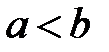 . Тогда существуют
. Тогда существуют 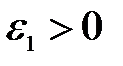 ,
, 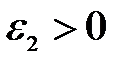 такие, что
такие, что  окрестность точки
окрестность точки 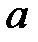 при пересечении с
при пересечении с 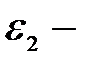 окрестностью точки
окрестностью точки 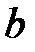 дает пустое множество: U
дает пустое множество: U 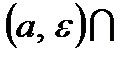 U
U  .
.
Доказательство:
I. 1. Если  ℝ, то возьмем
ℝ, то возьмем 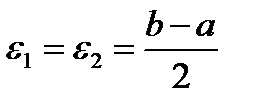 при
при 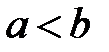 .
.
2. Получим такие окрестности точек  и
и  :
:
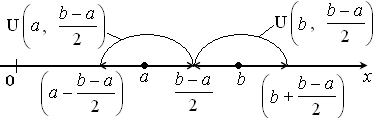
3. Очевидно, что окрестности не пересекаются.
II. 1. Если  ℝ, а
ℝ, а 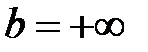 , то в качестве
, то в качестве  подходят:
подходят: 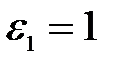 ,
,  .
.
2. Получим такие окрестности точек 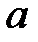 и
и  :
:

3. Очевидно, что окрестности не пересекаются.
III. 1. Если  ,
,  ℝ, то в качестве
ℝ, то в качестве  подходят:
подходят: 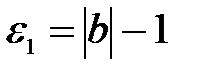 ,
, 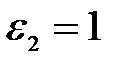 .
.
2. Получим такие окрестности точек 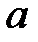 и
и  :
:
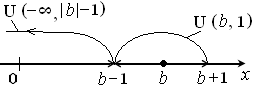
3. Очевидно, что окрестности не пересекаются.
IV. 1. Если  ,
,  , то при произвольном
, то при произвольном 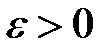 окрестности точки
окрестности точки 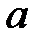 ,
,  не пересекаются.
не пересекаются.
2. Покажем это:

ч.т.д.
Замечание. Если 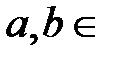 ℝ и
ℝ и 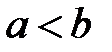 , то для двух любых
, то для двух любых  , таких что
, таких что 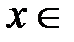 U
U  ,
, 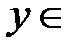 U
U 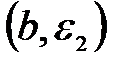 справедливо неравенство:
справедливо неравенство:  .
.
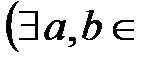 ℝ,
ℝ, 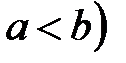
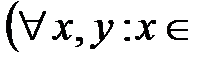 U
U  ,
, 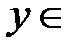 U
U  :
:  .
.
Примеры. Определить, какие множества заданы следующими неравенствами.
1. 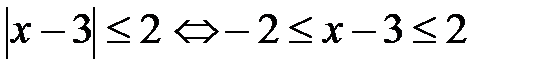 или
или  , т. е.
, т. е. 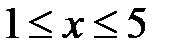 ;
; 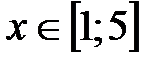 .
.
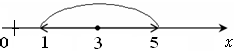
Ответ: отрезок 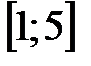 .
.
2. 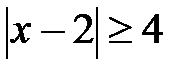

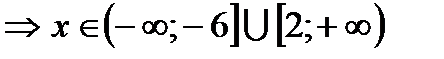 .
.
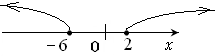
Ответ: объединение двух полуинтервалов 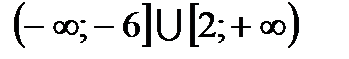 .
.
3. 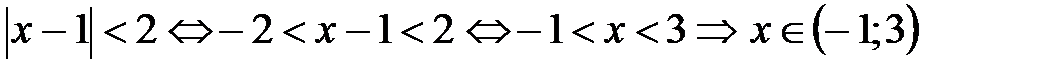 .
.

Ответ: интервал 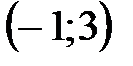 .
.
4. 



Ответ: объединение двух интервалов 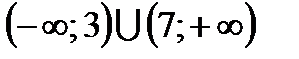 .
.
 2020-10-10
2020-10-10 412
412








