I. Ограниченный промежутки:
а) отрезки 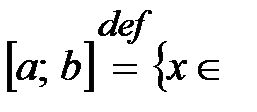 ℝ:
ℝ: 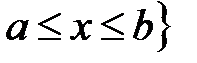 ,
, 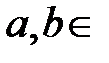 ℝ.
ℝ.
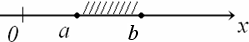
б) интервалы 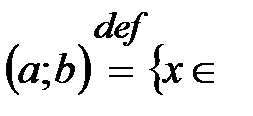 ℝ:
ℝ: 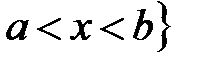 ,
, 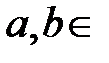 ℝ.
ℝ.
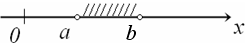
в) полуинтервалы:
1. 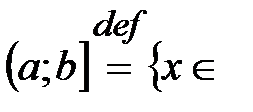 ℝ:
ℝ: 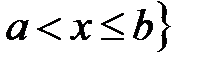 ,
, 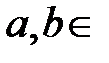 ℝ.
ℝ.
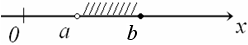
2. 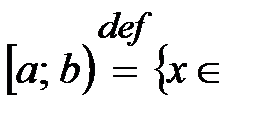 ℝ:
ℝ: 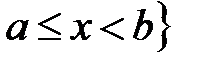 ,
, 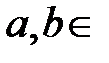 ℝ.
ℝ.
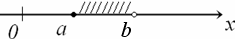
Замечание. В случае 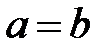 отрезок состоит из одной точки.
отрезок состоит из одной точки.
Определение 1. Интервал 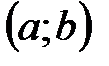 называется внутренностью отрезка
называется внутренностью отрезка 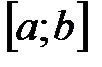 .
.
II. Неограниченные промежутки.
а) интервалы:
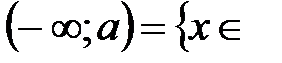 ℝ:
ℝ: 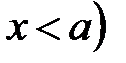 ,
, 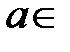 ℝ.
ℝ.
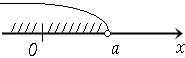
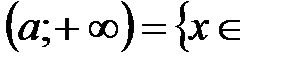 ℝ:
ℝ: 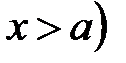 ,
, 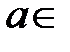 ℝ.
ℝ.
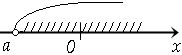
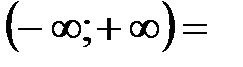 ℝ.
ℝ.
| 0 |
| х |
б) полуинтервалы:
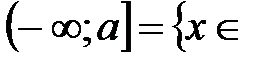 ℝ:
ℝ: 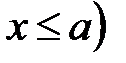 ,
, 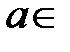 ℝ.
ℝ.
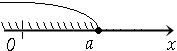
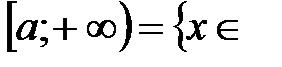 ℝ:
ℝ: 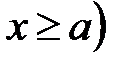 ,
, 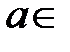 ℝ.
ℝ.
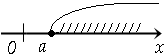
Определение 2. Отрезки, интервалы, полуинтервалы называются промежутками, а точки а, 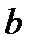 – их концами, а
– их концами, а 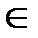 ℝ, b
ℝ, b 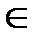 ℝ.
ℝ.
Определение 3. Если а и b – конечные числа, то действительное число 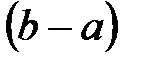 называется длиной промежутка с концами а и b.
называется длиной промежутка с концами а и b.
Определение 4. Если хоть одно из чисел а и b является бесконечным, то промежуток называется бесконечным.
Свойство промежутков всех типов расширенной числовой прямой.
Если точки 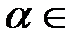 ℝ,
ℝ, 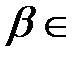 ℝ, причем
ℝ, причем 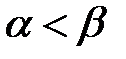 , принадлежат некоторому промежутку с концами
, принадлежат некоторому промежутку с концами 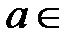 ℝ,
ℝ, 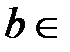 ℝ, то весь отрезок
ℝ, то весь отрезок 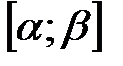 принадлежит этому промежутку.
принадлежит этому промежутку.
Примеры:
1. Из отрезка 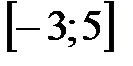 удален интервал
удален интервал 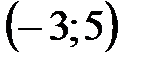 . Что осталось?
. Что осталось?
Ответ: Остались концы промежутка: точка 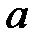 с координатой
с координатой 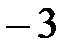 :
: 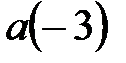 и точка
и точка 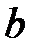 с координатой
с координатой 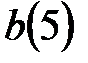 .
.
Или через множество: 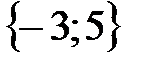 .
.
2. Из отрезка 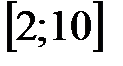 вырезан интервал
вырезан интервал 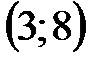 . Как записать множество оставшихся точек отрезка с помощью промежутков?
. Как записать множество оставшихся точек отрезка с помощью промежутков?
Ответ: 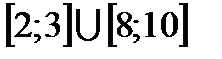 – отрезки.
– отрезки.
3. Из интервала 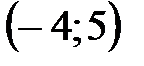 вырезаны два отрезка
вырезаны два отрезка 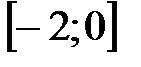 и
и 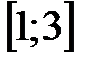 . Какие промежутки остались?
. Какие промежутки остались?
Ответ: 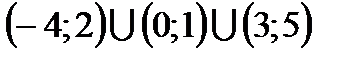 – остались такие интервалы.
– остались такие интервалы.
Понятие 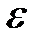 – окрестности
– окрестности
Определение. Если 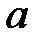 является действительным числом, то для любого
является действительным числом, то для любого 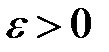
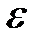 – окрестностью точки
– окрестностью точки 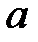 называется интервал
называется интервал 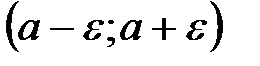 .
.
Обозначается 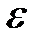 – окрестность так: U
– окрестность так: U 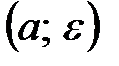
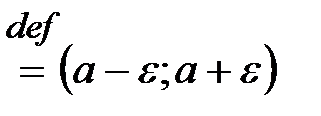 .
.
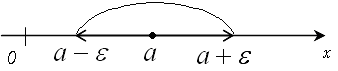
На координатной прямой:
1. Если 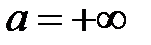 , то
, то 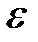 – окрестность точки
– окрестность точки 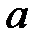 будет такой U
будет такой U 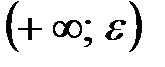
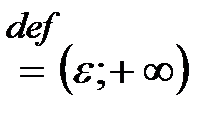 . Графически:
. Графически:
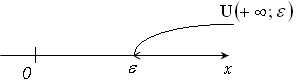
2. Если 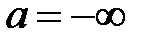 , то
, то 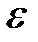 – окрестность точки
– окрестность точки 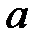 будет такой U
будет такой U 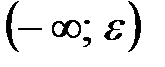
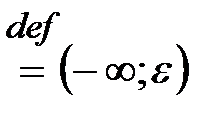 . Графически:
. Графически:
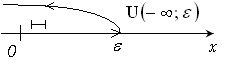
Замечание 1. При определении 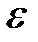 – окрестности бесконечно удаленных точек
– окрестности бесконечно удаленных точек 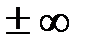 можно брать не только положительные
можно брать не только положительные 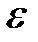 , но и любые
, но и любые 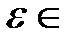 ℝ. Условие
ℝ. Условие 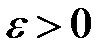 накладывается лишь с целью единообразия определений.
накладывается лишь с целью единообразия определений.
Замечание 2. В общем случае 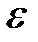 – окрестность точки
– окрестность точки 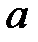 может быть записано неравенством
может быть записано неравенством 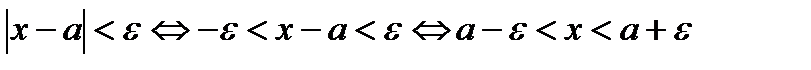 или
или 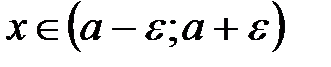 , где
, где 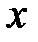 – множество действительных чисел.
– множество действительных чисел.
Пример. Дано неравенство 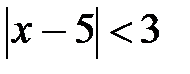 . О чем говорит это неравенство?
. О чем говорит это неравенство?
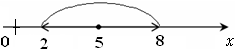
Множество действительных чисел 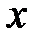 , удовлетворяющих неравенству
, удовлетворяющих неравенству 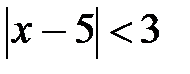 есть окрестность точки 5 радиусом 3.
есть окрестность точки 5 радиусом 3. 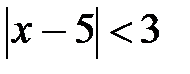 здесь
здесь 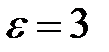 ,
, 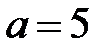 .
.
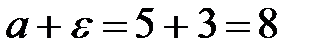
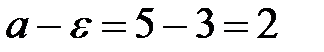
Модуль
Тема №1
 2020-10-10
2020-10-10 639
639








