Свойства точных граней множества

1. Свойство точной верхней грани множества:

Как бы ни было мало число 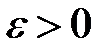, найдется такое число 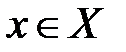, что справедливо будет неравенство: .

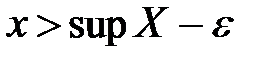Если такое число 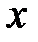 не найдется, то число  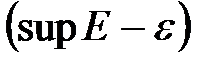станет точной верхней гранью множества 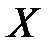. А число  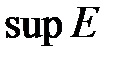перестанет быть точной верхней гранью, т.е. наименьшим из всех чисел, ограничивающих сверху множества .

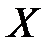Другими словами свойство точной верхней грани: число 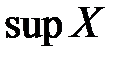 является наименьшим среди чисел, ограничивающих сверху множество 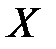, и оно не может быть еще уменьшено.

Пример. Пусть множество 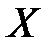 ограничено сверху и .

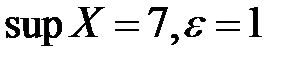Тогда число 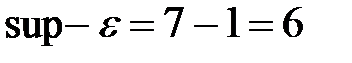. Значит, элемент множества число .

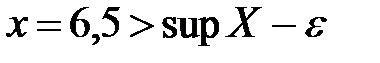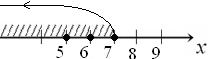
А для всех элементов этого множества выполняется неравенство: 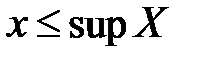. Следовательно, число  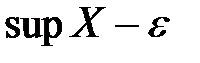не может быть точной верхней гранью.

2. Свойство точной нижней грани множества.

Как бы ни было мало число 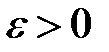, найдется такое число 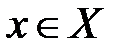, что будет выполняться неравенство: 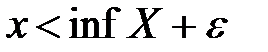, т.е. число  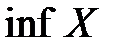является наибольшим и не может увеличено еще даже на .

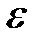Пример. Пусть множество 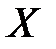 ограничено снизу и , .

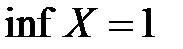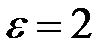Значит, число .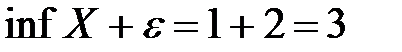

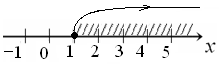
Тогда элементы 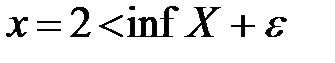, , 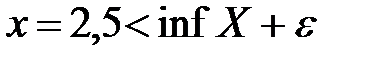а для всех элементов множества  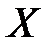должно выполняться неравенство .

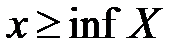3. Теорема. Всякое ограниченное сверху непустое числовое множество имеет точную верхнюю грань, а всякое ограниченное снизу непустое числовое множество имеет точную нижнюю грань.

Доказательство:

1. Пусть 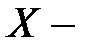 непустое числовое множество, ограниченное сверху.

2. Тогда множество 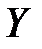, ограничивающее множество 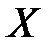сверху, также будет непустым.

3.Из определения верхней грани следует, что для 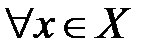 и 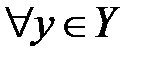 имеет место неравенство: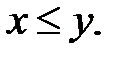

4. В силу свойства непрерывности действительных чисел существует такое число 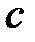, что для любых  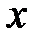и 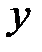 выполняется неравенство: 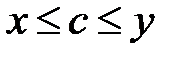. (1)

5. Из левой части неравенства (1) следует, что число 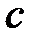 ограничивает множество  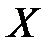сверху.

6. Из правой части неравенства (1) следует, что число 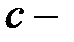 наименьшее из чисел, ограничивающих множество 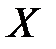, следовательно, число  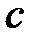является точной верхней гранью: .

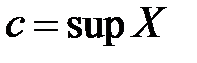ч.т.д.

Замечание. Случай существования точной нижней грани доказывается аналогично.