2020-10-10
80
Литература: [1]‚ гл. І‚ § 3
[2]‚ § 6
[9]‚ гл.·3‚ § 3.3
Скалярным произведением двух векторов 
и 
называется число, равное произведению модулей этих векторов на косинус угла между ними 
.
Свойства скалярного произведения:
1) 
(коммутативность);
2) 
(дистрибутивность);
3) 
, если 
или 
, или перпендикулярно ;
4) 
.
Первые три свойства показывают, что скалярное умножение суммы векторов на другую сумму можно производить по обычному правилу умножения многочленов.
Найдем выражение скалярного произведения векторов 
и 
в декартовых координатах. Для этого запишем разложение векторов и в базисе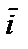 
, 
, 
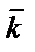и с учетом свойства скалярного произведения получим
Учитывая, что
получим
Таким образом, скалярное произведение равно сумме произведений одноименных координат.
Скалярное произведение векторов используется при решении ряда задач:
1) нахождение угла между векторами и :
;
2) вычисление проекции одного вектора на направление другого вектора:
;
3) проверка перпендикулярности двух векторов:
׀ 
, т.е. 
;
4) вычисление работы постоянной силы 
вдоль прямолинейного участка пути (вектор перемещения 
):
.
Пример 13. Даны векторы 
и 
. Найти проекцию вектора 
на направление вектора 
.
Решение. Вначале найдем координаты вектора 
:
.
Затем, используя скалярное произведение, вычислим проекцию вектора на направление вектора :
.
Пример 14. Даны вершины четырехугольника А (1, 2, 3), В (7, 3, 2), С (-3, 0, 6) и D (9, 2, 4) Доказать, что его диагонали АС и ВD взаимно перпендикулярны.
Решение. Определим координаты векторов 
'и 
:
, 
.
Проверяем условие перпендикулярности ненулевых векторов 
:
.
Так как скалярное произведение векторов 'и равно 0, они взаимно перпендикулярны.
Пример 15. Даны вершины треугольника А (3, 2, -3), В (5, 1, -1) и С (1, -2, 1). Найти внутренний угол при вершине А.
Решение. Искомый угол φ есть угол между векторами 
'и 
. Найдем координаты этих векторов:
,
.
Используя скалярное произведение, находим угол φ:
,
.
