Векторное произведение двух векторов

 

Литература: [1]‚ гл. I‚ § 3

[2]‚ § 12

[9]‚ гл.·3‚ § 3.4

 

Векторным произведение вектора  на вектор  называется такой вектор 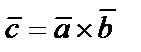, который удовлетворяет следующим условиям:

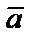
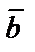
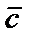
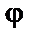
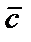1) модуль вектора  равен произведению модулей векторов  и  на синус угла между ними

,

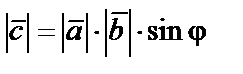т.е.  модуль  вектора 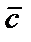  численно  равен  площади параллелограмма, построенного на векторах  и  как на сторонах;

2) вектор 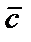 перпендикулярен векторам  и ;

3) вектор 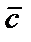 направлен так, что с конца вектора  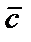кратчайший поворот от  к  виден происходящим против часовой стрелки.

Свойства векторного произведения:

1) векторное произведение некоммутативно (неперестановочно), при этом ;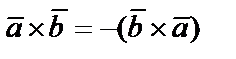

2) для векторного произведения выполняется дистрибутивный (распределительный) закон ;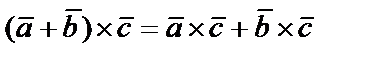

3) 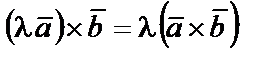, где 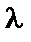 − любое действительное число;

4) 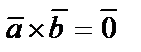, если векторы  и  коллинеарны или по крайней мере один из сомножителей является нулевым вектором.

Из первых трех свойств следует, что векторное умножение суммы векторов на сумму векторов подчиняется обычным правилам перемножения многочленов (но порядок следования множителей ввиду некоммутативности векторного произведения меняться не должен).

Найдем векторное произведение векторов  и  в декартовых координатах.

.

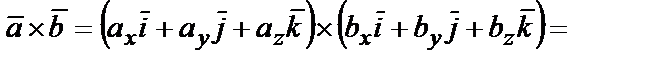
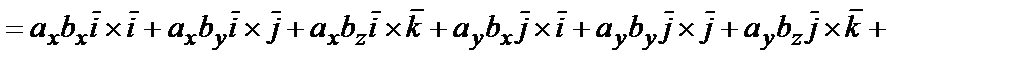
Учитывая, что ,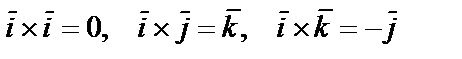

,

,

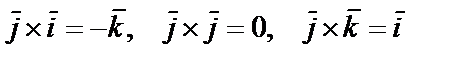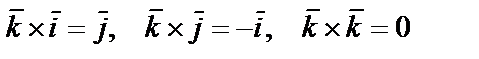получим

.

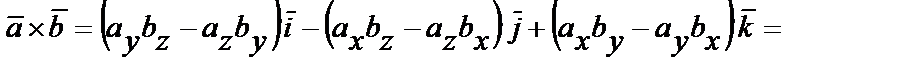
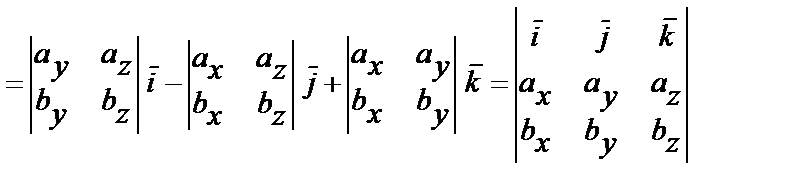Векторное произведение используется при решении ряда задач.

Площадь параллелограмма, построенного на векторах  и  равна модулю их векторного произведения 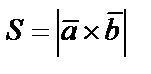, а площадь треугольника, построенного на векторах  и , равна .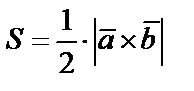

Пример 16. Вычислить площадь параллелограмма, три вершины которого находятся в точках А (4, 3, 2), В (2, 3, 4) и С (1, 1, 1).

Решение. Данный параллелограмм построен на векторах

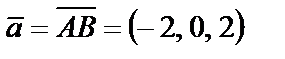 и .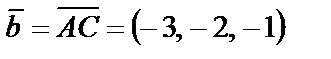

Его площадь равна модулю векторного произведения 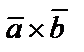. Находим векторное произведение

.

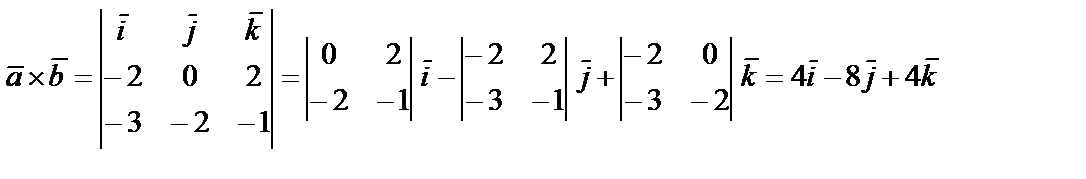Следовательно, площадь параллелограмма равна

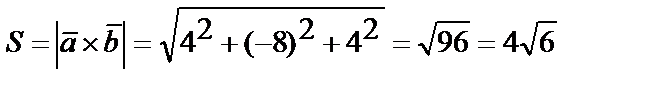(ед²).