Литература: [1]‚ гл. I‚§§ 1, 2
[2]‚ § 5
[9]‚ гл.·3‚ § 3.2
Вектор  называется линейной комбинацией векторов
называется линейной комбинацией векторов 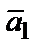 ,
, 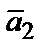 ,…,
,…, 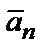 , если его можно представить в виде
, если его можно представить в виде 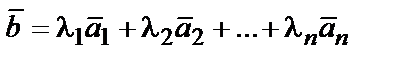 , где
, где 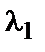 ,
, 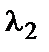 ,…,
,…, 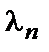 − некоторые числа. Это равенство называют также разложением вектора
− некоторые числа. Это равенство называют также разложением вектора  по векторам
по векторам 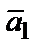 ,
, 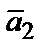 ,…,
,…, 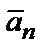 .
.
Векторы 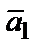 ,
, 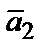 ,…,
,…, 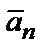 являются линейно зависимыми, если хотя бы один из них является линейной комбинацией остальных. Например,
являются линейно зависимыми, если хотя бы один из них является линейной комбинацией остальных. Например, 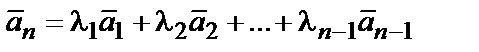 . В противном случае (т.е. ни один из векторов
. В противном случае (т.е. ни один из векторов 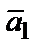 ,
, 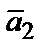 ,…,
,…, 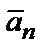 не может быть представлен в виде линейной комбинации остальных) векторы являются линейно независимыми.
не может быть представлен в виде линейной комбинации остальных) векторы являются линейно независимыми.
Пара векторов на плоскости является линейно зависимой тогда и только тогда, когда эти векторы коллинеарные.
Тройка векторов в пространстве является линейно зависимой тогда и только тогда, когда эти векторы компланарны.
Базисом на плоскости называется упорядоченная пара линейно независимых (т.е. неколлинеарных) векторов. Упорядоченная пара векторов означает, что указано, какой из этих векторов является первым, а какой вторым.
Базисом в пространстве называется упорядоченная тройка линейно независимых (т.е. некомпланарных) векторов.
Каждый вектор может быть представлен как линейная комбинация базисных векторов и притом единственным образом.
Например, 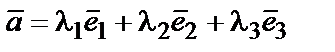 . Здесь
. Здесь 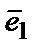 ,
, 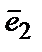 ,
, 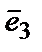 − базисные векторы. Коэффициенты
− базисные векторы. Коэффициенты 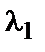 ,
, 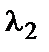 ,
, 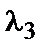 разложения вектора по базисным векторам называются координатами вектора в этом базисе.
разложения вектора по базисным векторам называются координатами вектора в этом базисе.
В трехмерном пространстве широко применяется декартова (прямоугольная) система координат Oxyz с базисными векторами 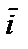 ,
,  ,
, 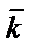 . Эти векторы ортогональны (т.е. взаимно перпендикулярны) и нормированы (т.е. имеют длину равную 1). Базис
. Эти векторы ортогональны (т.е. взаимно перпендикулярны) и нормированы (т.е. имеют длину равную 1). Базис 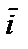 ,
,  ,
, 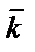 поэтому называется ортонормированным.
поэтому называется ортонормированным.
Любой вектор  в декартовой системе координат может быть единственным образом представлен в виде
в декартовой системе координат может быть единственным образом представлен в виде 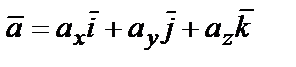 .
.
Особенность декартовой системы координат в том, что коэффициенты этого разложения 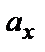 ,
, 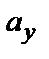 ,
, 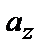 (т.е. координаты вектора) являются проекциями вектора
(т.е. координаты вектора) являются проекциями вектора  на соответствующие оси Ox, Oy и Oz.
на соответствующие оси Ox, Oy и Oz.
Длина (модуль) вектора определяется по формуле:
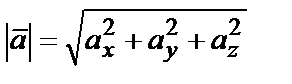 .
.
Направление вектора  задается углами α, β, γ, образованными ими с координатными осями Ox, Oy и Oz. Косинусы этих углов (они называются направляющими косинусами вектора) определяются по формулам:
задается углами α, β, γ, образованными ими с координатными осями Ox, Oy и Oz. Косинусы этих углов (они называются направляющими косинусами вектора) определяются по формулам:
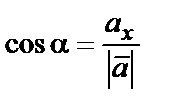 ,
, 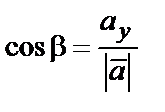 ,
, 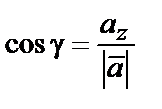 .
.
Направляющие косинусы связаны соотношением
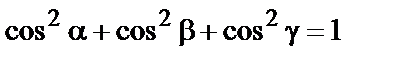 .
.
Если векторы  и
и  коллинеарные и сонаправленные, то их направляющие косинусы равны:
коллинеарные и сонаправленные, то их направляющие косинусы равны:
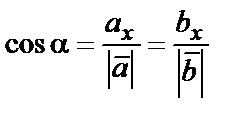 ,
, 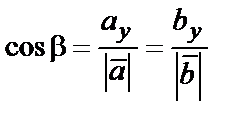 ,
, 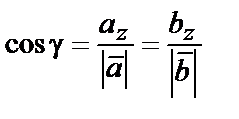 .
.
Откуда, введя обозначение 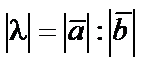 , получим условия коллинеарности векторов
, получим условия коллинеарности векторов  и
и  :
:
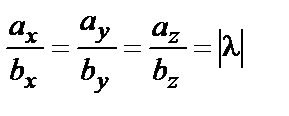 .
.
Заметим, что если векторы  и
и  противоположно направлены, то в равенстве следует перед
противоположно направлены, то в равенстве следует перед 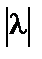 поставить знак минус.
поставить знак минус.
Если вектор задается направленным отрезком 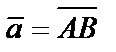 , причем
, причем 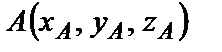 и
и 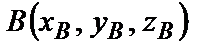 , то координаты вектора равны разности соответствующих координат точек конца и начала вектора
, то координаты вектора равны разности соответствующих координат точек конца и начала вектора
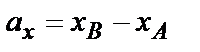 ,
, 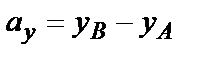 ,
, 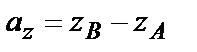 ,
,
при этом длина вектора определяется следующим образом
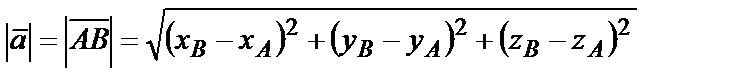 .
.
При сложении векторов в прямоугольной системе координат их координаты складываются
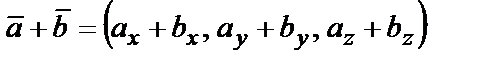 .
.
При умножении вектора на число координаты получаемого вектора умножаются на это число
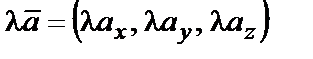 .
.
Пример 11. Вектор  составляет с осями координат острые углы α, β, γ, причем α = 45˚, β = 60˚. Найти его координаты, если
составляет с осями координат острые углы α, β, γ, причем α = 45˚, β = 60˚. Найти его координаты, если 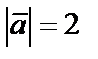 .
.
Решение. Прежде всего, найдем угол 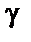 . C учетом того, что угол
. C учетом того, что угол 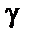 острый, имеем
острый, имеем
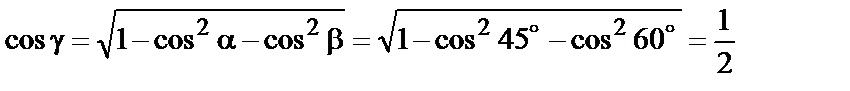 ,
, 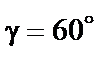 .
.
Искомые координаты вектора
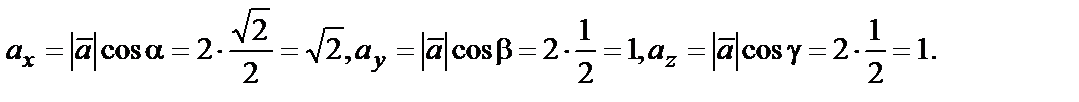
Итак, 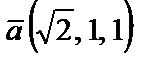 .
.
 2020-10-10
2020-10-10 127
127








