ВЕКТОРНАЯ АЛГЕБРА
Литература: [1]‚Улитин Г.М.,Гончаров А. Курс лекций по высшей математике.с. 18-31, лекции 4-6
[2]‚ Улитин Г.М Краткий курс высшей математики (есть на сайте кафедры ВМ Доннту)
[3] Герасимчук В.С. и др. Курс классической математики в примерах и задачах,часть1]
[4] Данко, Попов, Кожевникова. Высшая математика в примерах и задачах. Ч1
В природе существует два рода величин: скалярные и векторные. Величины, которые полностью определяются своим численным значением, называются скалярными (температура, путь, масса, объем, электрический заряд, работа и т.д.). Величины, для задания которых необходимо знать не только их численное значение, но и направление в пространстве, называются векторными (сила, действующая на тело, перемещение, скорость, ускорение, момент вращения и т.д.).
Вектор − это направленный отрезок. Векторы обозначаются  или
или 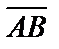 , где
, где  − начало вектора,
− начало вектора, 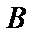 − его конец. Длина вектора называется его модулем и обозначается
− его конец. Длина вектора называется его модулем и обозначается 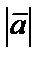 или
или 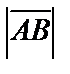 .
.
Коллинеарные векторы − это векторы, направления которых совпадают или противоположны, что обозначают  ׀׀
׀׀  .
.
Компланарные векторы − это векторы, лежащие в параллельных плоскостях, в частности, в одной плоскости.
Два вектора  и
и  называются равными, если они имеют одинаковую длину и одинаково направлены. Обозначают
называются равными, если они имеют одинаковую длину и одинаково направлены. Обозначают 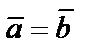 .
.
Рассмотрим линейные операции над векторами.
Суммой векторов  и
и  называется вектор, идущий из начала вектора
называется вектор, идущий из начала вектора  в конец вектора
в конец вектора  при условии, что начало вектора
при условии, что начало вектора  находится в конце вектора
находится в конце вектора  .
.
Это правило называют правилом треугольника (рис. 2.1, а) или параллелограмма (рис. 2.1, б) сложения векторов.
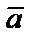
|

|
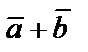
|
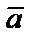
|

|
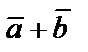
|
а) б)
Рис. 2.1 Сложение векторов
по правилу треугольника (а) и параллелограмма (б)
Понятие суммы векторов позволяют ввести:
1) операцию, обратную операции сложения, − разность векторов  и
и  как вектор
как вектор  такой, который в сумме с вектором
такой, который в сумме с вектором  дает вектор
дает вектор  (рис. 2.2, а),
(рис. 2.2, а),
2) сложение произвольного конечного числа векторов 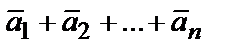 (правило многоугольника) (рис. 2.2, б).
(правило многоугольника) (рис. 2.2, б).
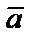
|

|
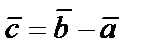
|
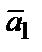
|
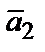
|
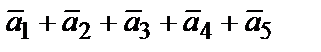
|
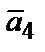
|
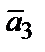
|

|
а) б)
Рис.2.2 Вычитание векторов (а) и
сложение векторов по правилу многоугольника (б)
Произведением вектора  на число λ называется такой вектор
на число λ называется такой вектор  , который удовлетворяет условиям:
, который удовлетворяет условиям:
а) 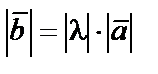 ;
;
б) векторы  и
и  − сонаправленные, если число λ > 0, и противоположно направленные, если λ < 0.
− сонаправленные, если число λ > 0, и противоположно направленные, если λ < 0.
Таким образом, из определения операции умножения вектора на число следует, что векторы  и
и  = λ
= λ  или сонаправленные или противоположно направленные, т.е. коллинеарные.
или сонаправленные или противоположно направленные, т.е. коллинеарные.
 2020-10-10
2020-10-10 118
118







