Следующая серия задач решается с помощью формул Коши:
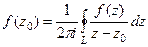 и
и 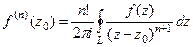 .
.
Здесь будут комбинированные задачи, состоящие из нескольких подзадач, где контур проводится сначала вокруг той или иной точки разрыва, а затем вокруг всех этих точек.
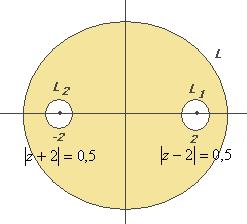
Задача 41. Вычислить  , где контур
, где контур  :
:
А) 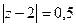 Б)
Б) 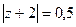 В)
В) 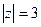 .
.
Решение. В знаменателе разложим на множители, и станет видно, что корни многочлена там 2 и  .
.
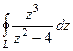 =
= 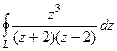 .
.
Если контур радиуса 0,5 окружает одну из точек, то надо применить интегральную формулу Коши, где точка 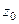 одна из них, а именно, в первом пункте
одна из них, а именно, в первом пункте 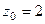 , а во втором
, а во втором 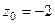 . Надо убрать из знаменателя соответствующую скобку, и присвоить конкретное
. Надо убрать из знаменателя соответствующую скобку, и присвоить конкретное 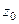 вместо
вместо 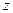 в оставшейся части функции.
в оставшейся части функции.
А) 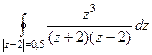 =
=  =
= 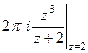 =
= 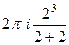 =
=  =
= 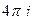 .
.
Б) 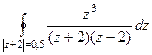 =
= 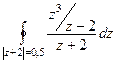 =
=  =
= 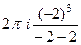 =
= 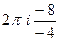 =
= 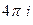 .
.
В) В третьем пункте, где контур окружает уже обе точки, достаточно будет воспользоваться теоремой Коши и суммировать результаты двух предыдущих пунктов. Получится 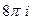 .
.
Ответы. А) 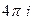 Б)
Б)  В)
В) 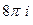 .
.
Задача 42. Вычислить 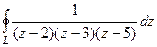 , где контур
, где контур  :
:
А) 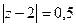 Б)
Б) 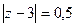 В)
В) 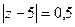 Г)
Г) 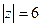 Д)
Д)  .
.
Решение. В каждом случае применяем интегральную формулу Коши к той или иной точке разрыва функции, 2, 3 и 5. Убирая соответствующий множитель из знаменателя, затем подставляем в оставшуюся часть функции это число.
А) 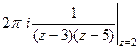 =
=  =
= 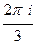 .
.
Б) 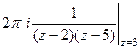 =
= 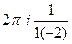 =
= 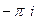 .
.
В) 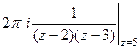 =
= 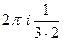 =
= 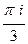 .
.
Если радиус 6, то все 3 точки находятся внутри контура. Суммируем все 3 результата:
Г) 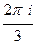
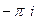 +
+ 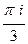 = 0.
= 0.
В последнем случае, лишь две из трёх точек внутри контура:
Д) 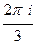
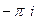 =
= 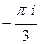 .
.
Ответы. А) 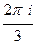 Б)
Б) 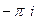 В)
В) 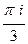 Г) 0 Д)
Г) 0 Д) 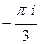 .
.
Задача 43. Вычислить 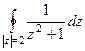 .
.
Решение. 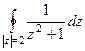 =
= 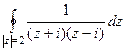 . Здесь две особые точки, это
. Здесь две особые точки, это  , они являются полюсами 1 порядка. Тогда в каждой из этих точек применим интегральную формулу Коши.
, они являются полюсами 1 порядка. Тогда в каждой из этих точек применим интегральную формулу Коши.
 =
=  =
=
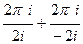 =
= 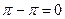 .
.
Ответ. 0.
Задача 44. Вычислить 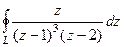 , где контур
, где контур  :
:
А) 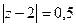 Б)
Б) 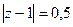 В)
В) 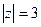 .
.
Решение.
А) 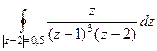 =
= 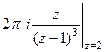 =
= 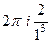 =
= 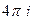 .
.
Б) В этом случае корень знаменателя имеет кратность 3, так что придётся считать с помощью 2-й производной.
Конкретизируем обобщённую формулу Коши для 3 степени:
 , при n=2:
, при n=2: 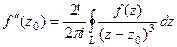 . Тогда
. Тогда 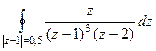 =
=  =
=
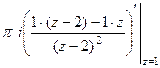 =
= 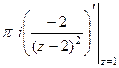 =
= 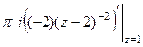 =
= 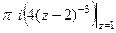 =
=  =
= 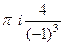 =
= 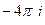 .
.
В) 
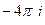 = 0.
= 0.
Ответы. А) 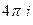 Б)
Б) 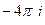 В) 0.
В) 0.
Задача 45. Вычислить  , где контур
, где контур  :
:
А)  Б)
Б) 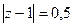 В)
В)  .
.
Решение.
А) 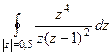 =
= 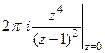 =
= 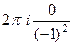 = 0.
= 0.
Б) 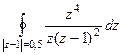 =
= 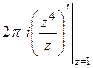 =
= 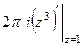 =
=  =
= 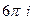 .
.
В) 0+ 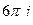 =
= 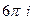 .
.
Ответы. А) 0 Б) 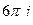 В)
В)  .
.
Задача 46. Вычислить 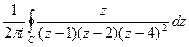 , где контур
, где контур 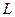 :
:
А) 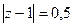 Б)
Б) 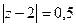 В)
В) 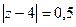 Г)
Г) 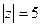 .
.
Решение. Так как здесь в интеграле уже изначально есть множитель  , то домножать на
, то домножать на 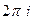 в правой части не нужно.
в правой части не нужно.
А) 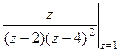 =
=  =
= 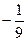 .
.
Б) 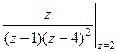 =
= 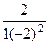 =
= 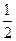 .
.
В) В отличие от двух первых точек, здесь в знаменателе корень 2-го порядка, поэтому подставляем 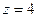 не сразу, а после вычисления производной.
не сразу, а после вычисления производной.
 =
= 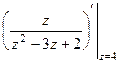 =
= 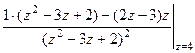 =
= 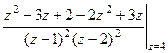 =
= 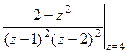 =
=  =
= 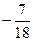 .
.
Г) По интегральной теореме Коши, сумма интегралов по трём предыдущим контурам: 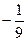 +
+ 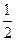
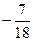 = 0.
= 0.
Ответы. А) 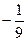 Б)
Б) 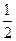 В)
В) 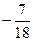 Г) 0.
Г) 0.
Задача 47. Вычислить 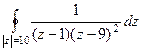 .
.
Решение. Здесь две особые точки, 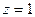 полюс 1-го порядка и
полюс 1-го порядка и 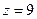 полюс 2-го порядка. Для 2-й точки надо применять обобщённую формулу Коши (с производной).
полюс 2-го порядка. Для 2-й точки надо применять обобщённую формулу Коши (с производной).
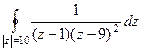 =
= 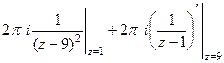 =
=
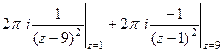 =
= 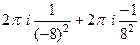 =
=
 .
.
Ответ. 0.
Задача 48. Вычислить 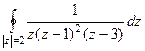 .
.
Решение. Внутри окружности радиуса 2 лежат 2 из 3 особых точек, а именно, 0 и 1, точка 3 снаружи.
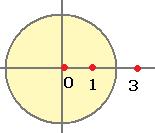
Поэтому интегральную формулу Коши применяем только к двум точкам.
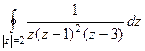 =
= 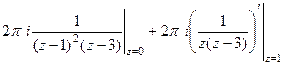 .
.
Предварительно вычислим производную.
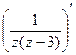 =
=  =
= 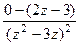 =
= 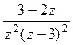 .
.
Далее, 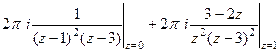 =
=
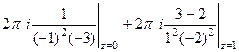 =
= 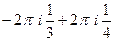 =
=
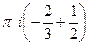 =
= 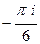 .
.
Ответ. 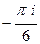 .
.
Задача 49. Вычислить 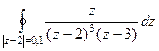 .
.
Решение. 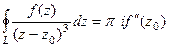 , тогда
, тогда 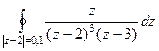 =
=  =
= 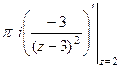 =
=  =
= 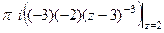 =
= 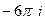
Ответ. 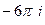 .
.
 2020-10-11
2020-10-11 131
131








