Заметив, что функция 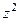 аналитическая, т.е. для неё выполняются условия Коши-Римана, можно не раскрывать скобки предыдущим способом, а вычислить первообразную по
аналитическая, т.е. для неё выполняются условия Коши-Римана, можно не раскрывать скобки предыдущим способом, а вычислить первообразную по  в начальной и конечной точке.
в начальной и конечной точке.
 =
=  =
= 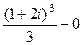 , а дальше всё сводится просто к вычислению степени комплексного числа.
, а дальше всё сводится просто к вычислению степени комплексного числа.

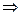
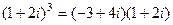 =
= 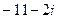 , тогда
, тогда
 =
= 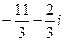 .
.
Ответ. 
Домашняя задача. Вычислить 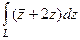 , где
, где  дуга параболы
дуга параболы 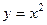 (от точки 0 до
(от точки 0 до  ). Ответ.
). Ответ. 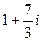 .
.
Задача 38. Вычислить  по участку единичной окружности в 1-й четверти от 1 до
по участку единичной окружности в 1-й четверти от 1 до 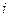 .
.
Решение. Здесь тоже можно вычислять как без, так и по формуле Ньютона-Лейбница. Но разница в объёме вычислений будет огромная.
Так как функция аналитическая, нам не важно, соединены точки по дуге окружности или по какой-то другой линии, на самом деле результат зависит только от первообразной в начальной и конечной точках. Сделаем по формуле Ньютона-Лейбница.
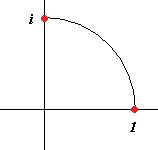
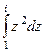 =
= 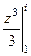 =
=  =
= 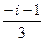 =
= 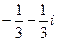 .
.
Ответ. 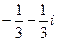 .
.
Для сравнения, № 38 можно решить в качестве домашней задачи и без формулы Ньютона-Лейбница.
Задача 39. Вычислить 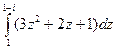 .
.
Решение. Здесь сумма степенных функций, они являются аналитическими. Поэтому используем формулу Ньютона-Лейбница.
 =
=  =
= 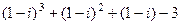 .
.
Отдельно вычислим 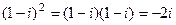 ,
,
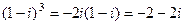 .
.
Тогда 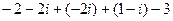 =
=  .
.
Ответ.  .
.
Задача 40. Вычислить 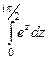 .
.
Решение. Можно применять формулу Ньютона-Лейбница, так как функция 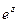 аналитическая.
аналитическая.
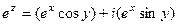 , тогда:
, тогда:
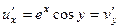 ,
, 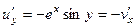 .
.
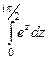 =
= 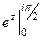 =
=  =
= 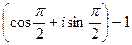 =
= 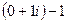 =
=
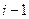 =
= 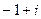 .
.
Ответ. 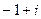 .
.
Домашняя задача. Вычислить 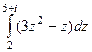 . Ответ.
. Ответ. 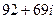 .
.
Решение.  =
= 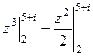 =
= 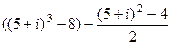 .
.
Вычислим квадрат и куб этого числа. 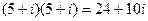 ,
,
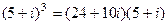 =
= 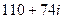 .
.
Тогда  =
= 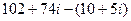 =
=
 . Ответ.
. Ответ.  .
.
Практика 5 (неделя с 28 сентября по 4 октября).
 2020-10-11
2020-10-11 180
180








