Задача 32. 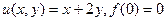 .
.
А. Найти 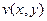 Б. Найти
Б. Найти 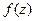 .
.
Решение. Проверим уравнение Лапласа.
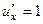
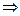
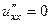 ,
, 
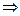
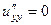 .
.
Сумма вторых производных равна 0.
Ищем 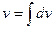 =
= 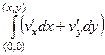 =
= 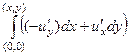 =
= 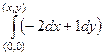 =
= 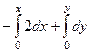 =
= 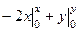 =
= 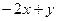 .
.
При произвольном выборе начальной точки, 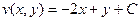 , из условия
, из условия 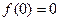 определим константу
определим константу 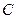 . Если
. Если 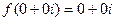 то
то 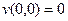 , тогда
, тогда 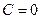 .
.
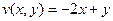 .
.
Итак, 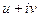 =
= 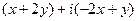 =
= 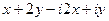 =
= 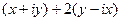 . Здесь можно даже не пользоваться формулами
. Здесь можно даже не пользоваться формулами 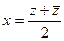 ,
, 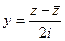 , ведь мы уже сумели получить
, ведь мы уже сумели получить 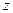 в первой скобке, а во 2-й
в первой скобке, а во 2-й 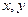 в обратном порядке и одна с минусом, если домножить и поделить на
в обратном порядке и одна с минусом, если домножить и поделить на 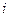 , то также удастся получить выражение с
, то также удастся получить выражение с 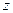 .
.
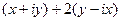 =
= 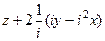 =
= 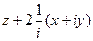 =
= 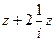 =
= 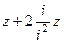 =
= 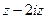 .
.
Для сравнения - старым методом:
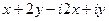 =
= 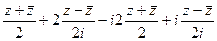 =
=
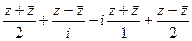 =
= 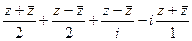 =
=
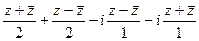 =
= 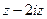 .
.
Ответ. 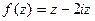 .
.
Интегрирование функций комплексного переменного
Задача 33. Вычислить 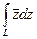 по отрезку от 0 до
по отрезку от 0 до 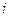 .
.
Решение. 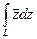 =
= 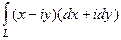 =
= 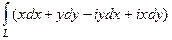 =
=
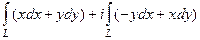 а это уже 2 криволинейных интеграла второго рода от различных векторных полей. Причём на вертикальном отрезке, соединяющем 0 с точкой
а это уже 2 криволинейных интеграла второго рода от различных векторных полей. Причём на вертикальном отрезке, соединяющем 0 с точкой 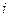 , фиксировано
, фиксировано 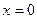 , а значит и
, а значит и 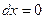 , т.е. исчезают все слагаемые, где есть
, т.е. исчезают все слагаемые, где есть 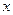 или
или 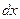 .
.
При этом 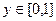 . Итак,
. Итак, 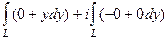 =
= 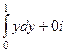 =
= 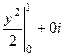 =
= 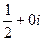 =
= 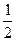 .
.
Ответ. 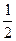 .
.
Задача 34. Вычислить 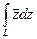 по окружности радиуса
по окружности радиуса 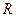 .
.
Решение. Изначально преобразование с раскрытием скобок точно такое же, как и в прошлой задаче: 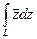 =
= 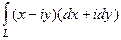 =
= 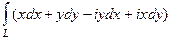 =
= 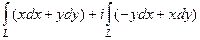 .
.
Дальше, криволинейные интегралы вычисляются иначе из-за того, что другая кривая. На окружности наилучший способ задать точку - параметрически: 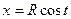 ,
, 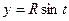 . При этом
. При этом 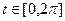 .
.
Также вычислим дифференциалы: 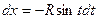 ,
, 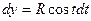 .
.
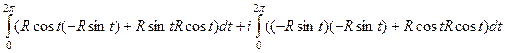 =
= 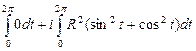 =
= 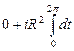 =
= 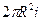 .
.
Ответ. 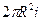 .
.
Задача 35. Вычислить 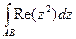 по отрезку от 0 до
по отрезку от 0 до 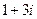 .
.
Решение. Так как 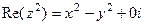 , то функция не аналитическая, т.к. частные производные от
, то функция не аналитическая, т.к. частные производные от 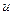 будут какие-то функции, а от
будут какие-то функции, а от 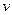 нулевые, и точно не будет совпадений, которые нужны для условий Коши-Римана. Поэтому формулу Ньютона-Лейбница здесь применить нельзя, а только универсальный способ с разложением на
нулевые, и точно не будет совпадений, которые нужны для условий Коши-Римана. Поэтому формулу Ньютона-Лейбница здесь применить нельзя, а только универсальный способ с разложением на 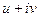 . Отрезок от (0,0) до (1,3), он характеризуется явным уравнением
. Отрезок от (0,0) до (1,3), он характеризуется явным уравнением 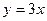 , при этом
, при этом 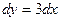 ,
, 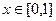 .
.
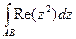 =
= 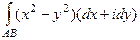 =
= 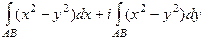 =
=
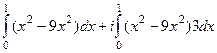 =
= 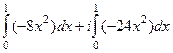 =
=
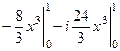 =
= 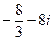 .
.
Ответ. 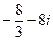 .
.
Задача 36. Вычислить 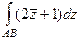 , где АВ - участок кубической параболы
, где АВ - участок кубической параболы 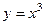 от (0,0) до (1,1).
от (0,0) до (1,1).
Решение. 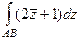 =
= 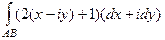 =
=
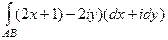 =
= 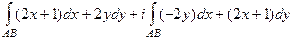 .
.
Теперь сведём все получившиеся криволинейные интегралы к одной лишь переменной 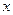 , заменяя
, заменяя 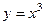 и
и 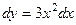 , где
, где 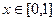 .
.
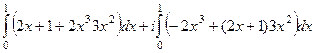 =
=
= 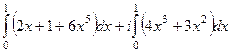 =
=
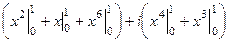 =
= 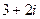 .
.
Ответ. 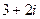 .
.
Задача 37. Вычислить 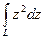 по отрезку от 0 до
по отрезку от 0 до 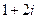 .
.
Решение. Способ 1. Без формулы Ньютона-Лейбница.
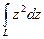 =
= 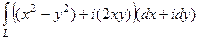 =
=
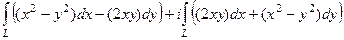 =
=
Далее используем явное выражение 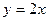 , так как отрезок соединяет точки (0,0) и (1,2). При этом
, так как отрезок соединяет точки (0,0) и (1,2). При этом 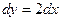 ,
, 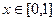 .
.
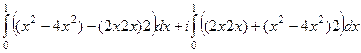 =
=
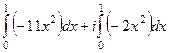 =
= 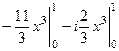 =
= 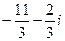 .
.
 2020-10-11
2020-10-11 139
139








