Вспомнить формулу: 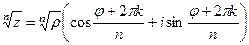 .
.
Задача 11. Вычислить  .
.
Решение. Для числа  :
: 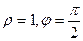 .
.
По формуле  получаем
получаем
 =
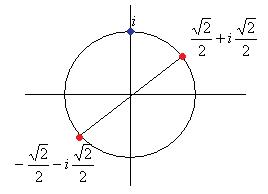
=  , значений будет всего 2.
, значений будет всего 2.
 :
:  =
=  ,
,
 :
:  =
=  .
.
Ответ. 
Задача 12. Вычислить  .
.
Решение. Сначала запишем число в тригонометрической форме.
 . Тогда
. Тогда

 =
=
 . Начертим окружность радиуса 2 и отметим там 6 точек, первой соответствует угол 300, остальные больше на 600, 1200 и так далее.
. Начертим окружность радиуса 2 и отметим там 6 точек, первой соответствует угол 300, остальные больше на 600, 1200 и так далее.


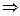

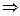

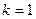

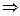


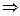

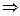


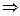

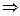







 .
.
Ответ.  и
и  .
.
Задача 13. Вычислить 
Решение. Формула: 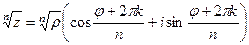 .
.
Сначала найдём модуль и аргумент исходного числа.
 (т.к. 90 градусов и ещё 30 во второй четверти),
(т.к. 90 градусов и ещё 30 во второй четверти),
 .
.
Тогда  =
=  =
=  таким образом, 4 точки лежат на окружности, углы 300, 1200, 2100, 3000 (по +900 добавить 4 раза). Отмечены на чертеже зелёным. Здесь 4 корня:
таким образом, 4 точки лежат на окружности, углы 300, 1200, 2100, 3000 (по +900 добавить 4 раза). Отмечены на чертеже зелёным. Здесь 4 корня:
 :
:  =
=  =
=  .
. 
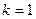 :
:  =
= 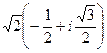 =
= 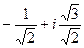 .
. 
 :
:  =
= 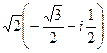 =
=  .
. 
 :
: 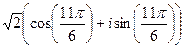 =
=  =
=  .
. 
Чертёж:

Ответ.  и
и  .
.
Функции комплексного переменного.
Задача 14. Дано  . Найти
. Найти  .
.
Решение. 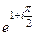 =
= 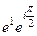 =
=  =
=  =
=  .
.
Ответ.  .
.
Задача 15. Дано  . Найти
. Найти  .
.
Решение.  =
=  =
=  . Далее с помощью прямоугольного треугольника вычислим
. Далее с помощью прямоугольного треугольника вычислим  . Если надо найти синус и косинус того угла, тангенс которого равен 3, то сначала подпишем длины катетов по известному тангенсу, гипотенуза
. Если надо найти синус и косинус того угла, тангенс которого равен 3, то сначала подпишем длины катетов по известному тангенсу, гипотенуза  вычислится автоматом по теореме Пифагора, а далее будет уже известны синус и косинус.
вычислится автоматом по теореме Пифагора, а далее будет уже известны синус и косинус.

 =
=  =
= 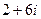 .
.
Ответ. 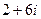 .
.
Задача 15-А. По формуле 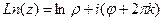 . вычислить
. вычислить  .
.
Решение. Найдём модуль и аргумент:  ,
,  . Тогда
. Тогда  =
=  .
.
Как видим, это обратная операция, т.е. с точностью до добавки  мы как раз и получили то, что было в условии исходной задачи.
мы как раз и получили то, что было в условии исходной задачи.
Если возвести экспоненту в степень любого из этих значений логарифма, в частности, 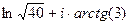 при
при  , то получится
, то получится 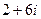 .
.
Задача 16. Дано 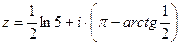 . Найти
. Найти  .
.
Решение.  =
=  =
=
 =
=
 . Делаем аналогично тому, как в прошлой задаче, просто треугольник здесь во 2 четверти (угол
. Делаем аналогично тому, как в прошлой задаче, просто треугольник здесь во 2 четверти (угол  отмеряется от 180 в обратном направлении).
отмеряется от 180 в обратном направлении).

Но гипотенуза всё равно легко вычисляется по теореме Пифагора:  , тогда
, тогда  =
=  .
.
Ответ.  .
.
Логарифм. Вспомнить формулу:  .
.
 , т.е. любое целое число.
, т.е. любое целое число.
Задача 17. Найти все значения  .
.
Решение. Используем формулу 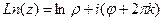 .
.
Для числа 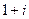 ,
,  ,
,  . Тогда
. Тогда
 .
.
Чертёж: бесконечная последовательность точек, на уровне абсциссы
 , по высоте каждая пара соседних отличается на
, по высоте каждая пара соседних отличается на  .
.

Ответ. 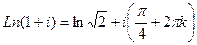 .
.
 2020-10-11
2020-10-11 136
136








