Возрастание и убывание функции.
Теорема 3.6. (Необходимые условия возрастания (убывания) функции)
Если дифференцируемая на интервале 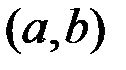 функция
функция 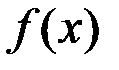 возрастает (убывает), то
возрастает (убывает), то  ,
,  (
( ,
,  .
.

Рис 3.3
Геометрически эта теорема означает, что касательные к графику возрастающей (убывающей) функции образуют острые углы с положительным направлением оси (для убывающей функции эти углы – тупые) или в некоторых точках параллельны оси  (см. Рис 3.3).
(см. Рис 3.3).
Теорема 3.7. (Достаточные условия возрастания (убывания) функции)
Если функция 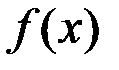 дифференцируемая на интервале
дифференцируемая на интервале 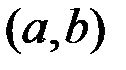 и
и  ,
,  , то эта функция
, то эта функция 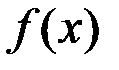 возрастает на интервале
возрастает на интервале 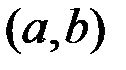 .
.
Если функция 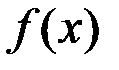 дифференцируемая на интервале
дифференцируемая на интервале 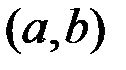 и
и  ,
,  , то эта функция
, то эта функция 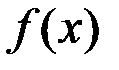 убывает на интервале
убывает на интервале 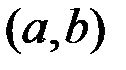 .
.
 2020-10-09
2020-10-09 178
178








