2020-10-09
441
Пусть 
и 
– дифференцируемые в некотором интервале 
функции.
Теорема 2.2. Производная суммы (разности) двух функций 
равна сумме (разности) производных этих функций: 
.
Теорема 2.3. Производнаяпроизведения 
двух функций равна произведению производной первой функции на второй сомножитель плюс произведение второго сомножителя на производной второй функции: 
.
Теорема 2.4. Производнаячастного двух функций 
, если 
равна дроби, числитель которой есть разность произведений знаменателя дроби на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего знаменателя дроби: 
.
Следствие 2.1. Если 
, то 
.
Следствие 2.2. Если , то 
.
Следствие 2.3. Если , то 
.
Таким образом, при вычислении производных следует применять следующие правила дифференцирования:
1. ;
2. ;
3. ;
4. , ;
Производная сложной и обратной функции
Пусть 
– сложная функция с промежуточным аргументом 
и независимым аргументом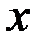 
, то есть 
и 
.
Теорема 2.5. (Производная сложной функции )
|
|
|
Если функция имеет производную 
в точке 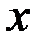, а функция имеет производную 
в соответствующей точке , то сложная функция имеет производную 
в точке 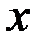, которая находится по формуле: 
.
З а м е ч а н и е 2.4. Для нахождения 
– производной сложной функции надо 
– производную данной функции по промежуточному аргументу умножить на 
– производную промежуточного аргумента по независимому аргументу.
Пусть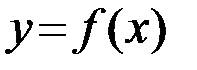 
и 
– взаимно обратные функции.
Теорема 2.6. (Производная обратной функции) Если функция 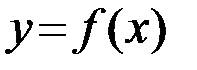строго монотонна на интервале и имеет неравную нулю производную 
в произвольной точке этого интервала, то обратная ей функция в соответствующей точке также имеет производную 
, определяемую равенством: 
или 
.
З а м е ч а н и е 2.5. Производная обратной функции равна обратной величине производной данной функции.
Производные основных элементарных функций
(таблица производных)
1. 
;
2. 
; 
; 
;
3. 
;
4. 
;
5. 
;
6. 
;
7. 
;
8. 
;
9. ;
10. ;
11. 
;
12. 
;
13. 
;
14. 
.
