2020-10-09
126
Функция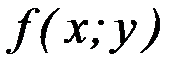 
называется однородной функцией 
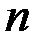-го порядка (измерения), если выполняется равенство
.
Например, функция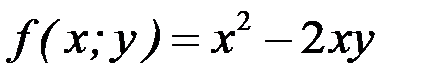 
есть однородная функция второго порядка, поскольку
.
Дифференциальное уравнение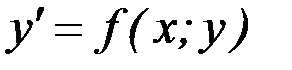 
называется однородным, если функция 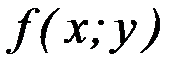есть однородная функция нулевого порядка.
Однородное ДУ можно представить в виде
. (7.4)
Однородное уравнение (7.4) преобразуется в уравнение с разделяющимися переменными при помощи подстановки
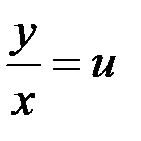или, что то же самое, 
.
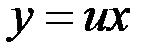Действительно, подставив 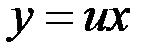и 
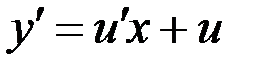в уравнение (7.4), получаем 
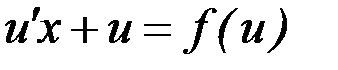или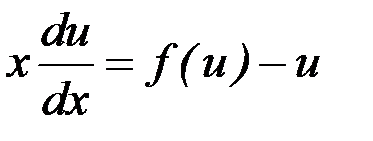 
, т.е. уравнение с разделяющимися переменными. Найдя его общее решение (или общий интеграл), следует заменить в нем 
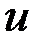на 
. Получим общее решение (интеграл) исходного уравнения.
Линейные уравнения
Дифференциальное уравнение называется линейным, если его можно записать в виде
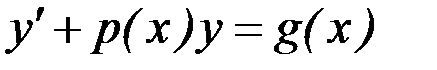, (7.5)
где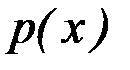 
и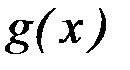 
– заданные функции или постоянные.
Особенность линейного ДУ: искомая функция 
и ее производная 
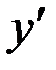входят в уравнение в первой степени, не перемножаясь между собой.
Решение уравнения (12.5) ищется в виде произведения двух функций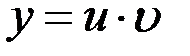 
, где 
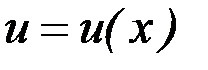и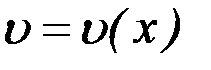 
– неизвестные функции от 
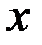, причем одна из них произвольна. Тогда 
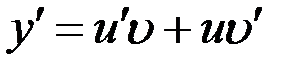. Подставляя выражения и в уравнение (12.5), получаем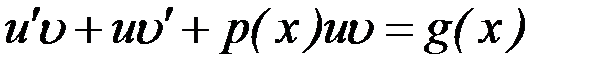 
или
. (7.6)
Подберем функцию так, чтобы выражение в скобках было равно нулю, т.е. решим ДУ с разделяющимися переменными
.
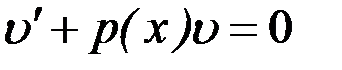
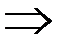
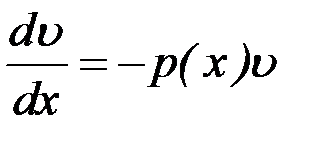
Интегрируя, получаем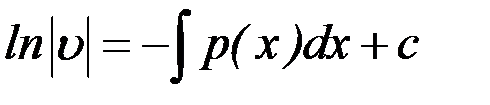 
.
Ввиду свободы выбора функции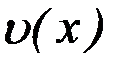 
, можно принять 
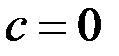. Тогда
.
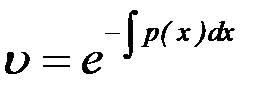Подставляя найденную функцию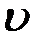 
в уравнение (7.6), получаем ДУ с разделяющимися переменными
.
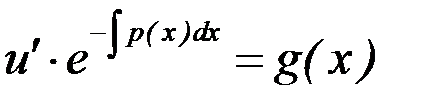
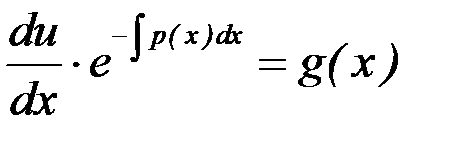
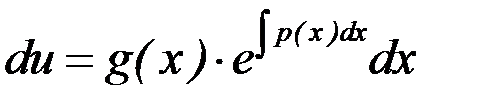
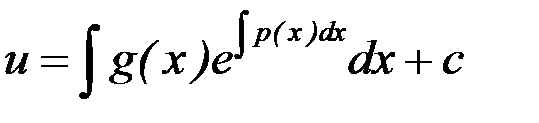Возвращаясь к переменной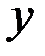 
, получаем решение исходного ДУ (7.5)
.
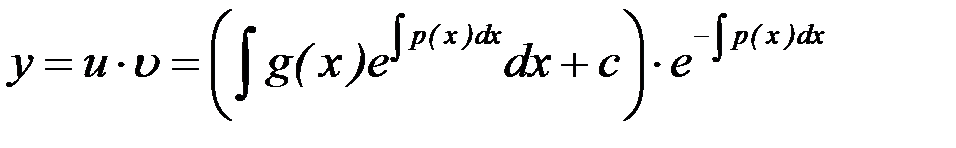Линейные дифференциальные уравнения второго порядка
