Интегральный признак Коши

 

Пусть все члены ряда

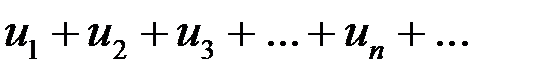                                 (8.6)

положительны и не возрастают, то есть

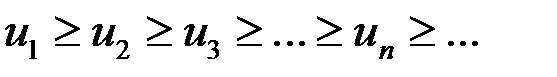
Пусть  – такая непрерывная невозрастающая на промежутке [1, ) функция, что 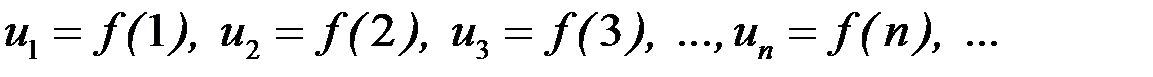 Тогда справедливы следующие утверждения:

1) если несобственный интеграл 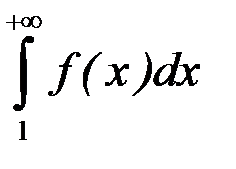 сходится, то сходится и ряд (8.6);

2) если несобственный интеграл 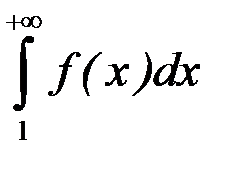 расходится, то расходится и ряд (8.6).

 

Знакопеременные и знакочередующиеся ряды

 

Ряд 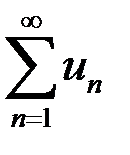 называется знакопеременным, если среди его членов имеются как положительные, так и отрицательные.

Знакопеременный ряд  называется абсолютно сходящимся, если ряд 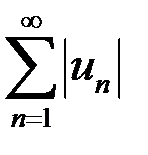 сходится.

Теорема 8.6. Если знакопеременный ряд абсолютно сходится, то он сходится.

Замечание 8.4. Обратное утверждение, вообще говоря, неверно.

Знакопеременный ряд  называется условно сходящимся, если он сходится, а ряд 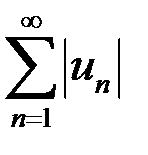 расходится.

Знакопеременный ряд вида

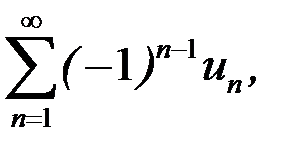                                          (8.7)

где 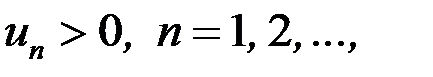 называется знакочередующимся.

Признак Лейбница. Если в знакочередующемся ряде (8.7) члены таковы, что

                               (8.8)

и

то ряд (13.7) сходится. При этом его сумма  удовлетворяет неравенствам:

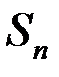Замечание 8.5. Если для ряда (8.7) выполнены условия признака Лейбница,  – его сумма,  – его 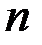-я частичная сумма, то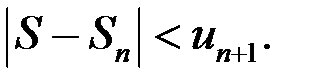

 

Замечание 8.6. Если в признаке Лейбница условие (8.8) заменить условием

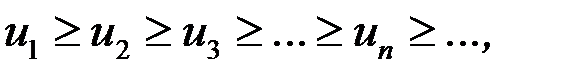
то ряд (8.7) будет сходиться. При этом для его суммы и его 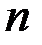-й частичной суммы  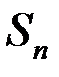будут выполняться неравенства:  

 

Понятие функционального ряда.