2020-10-09
151
1. Определенный интеграл с одинаковыми пределами интегрирования равен нулю: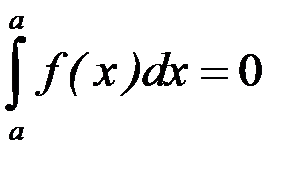 
.
2. По определению полагается: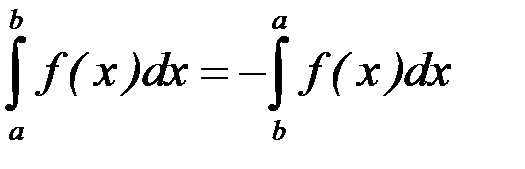 
.
3. Постоянный множитель можно выносить за знак определенного интеграла: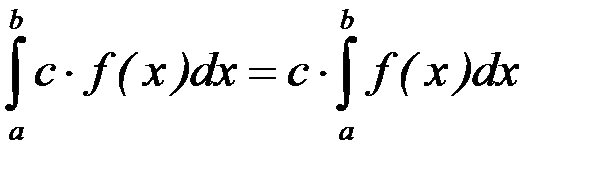 
.
4. Определенный интеграл от алгебраической суммы функций равен алгебраической сумме их определенных интегралов:
.
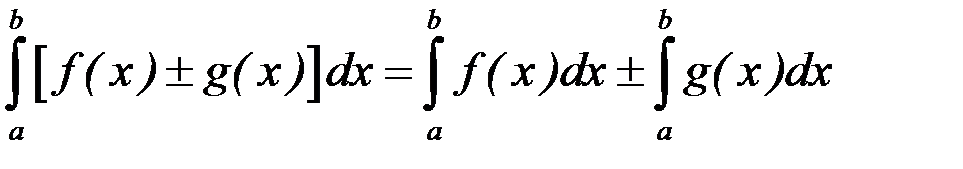5. Для любых чисел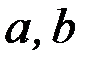 
и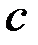 
имеет место равенство
.
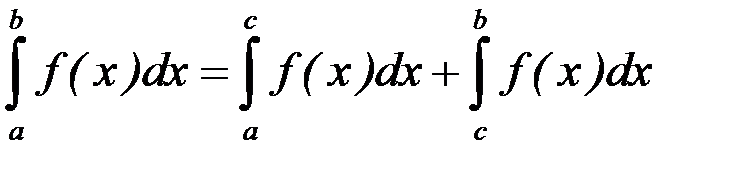6. Если функция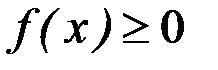 
всюду на отрезке 
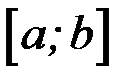, то
.
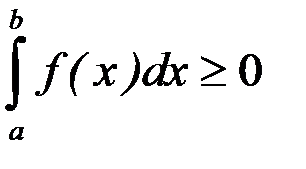7. Если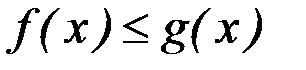 
всюду на отрезке 
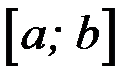, то
.
8. Если функция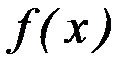 
интегрируема на 
, то
.
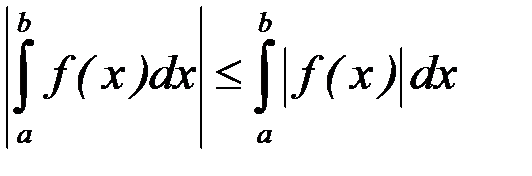9. Если 
и 
– соответственно максимум и минимум функции 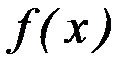на отрезке 
, то
.
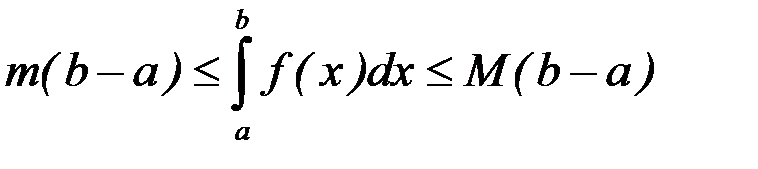10. «Теорема о среднем». Если функция 
непрерывна на отрезке 
, то существует точка 
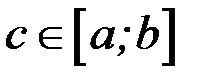такая, что
.
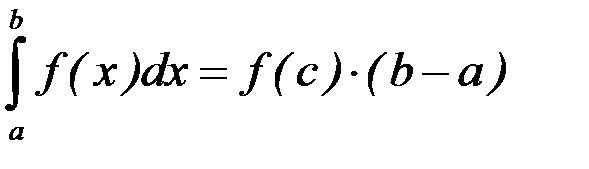Число 
называется средним значением функции на отрезке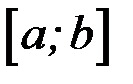 
.
Основная формула интегрального исчисления
Простым и удобным методом вычисления определенного интеграла от непрерывной функции является формулаНьютона-Лейбница:
.
Основные правила интегрирования
Замена переменной в определенном интеграле
Теорема 6.4. Пусть:
1) 
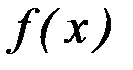– непрерывная функция на отрезке ;
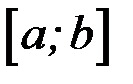2) функция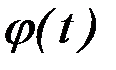 
– дифференцируема на 
,
– непрерывна на
и множеством значений функции 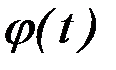является отрезок ;
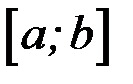3) 
.
Тогда справедлива формула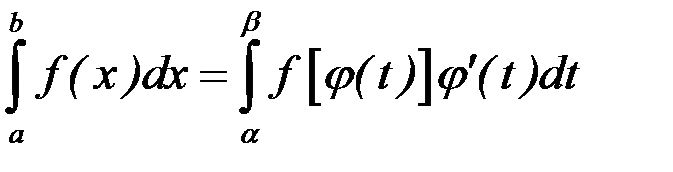 
, которая
называется формулой замены переменной в определенном интеграле.
Отметим, что:
1) при вычислении определенного интеграла с помощью замены переменной возвращаться к старой переменной не требуется;
2) часто вместо замены переменной 
применяют подстановку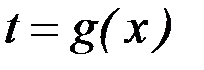 
;
3) не следует забывать менять пределы интегрирования при замене переменных!
Интегрирование по частям в определенном интеграле
Теорема 6.5. Пусть функци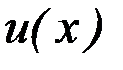и 
и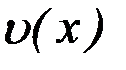 
имеют непрерывные производные на отрезке 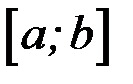; тогда справедлива формула
,
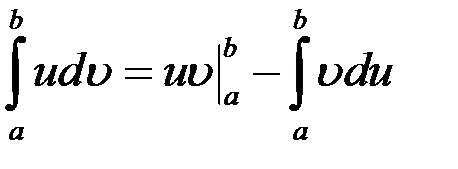которая называется формулой интегрирования по частям в определенном интеграле.
Геометрические приложения определенного интеграла
