2020-10-09
172
Теорема 8.4. Пусть заданы ряды
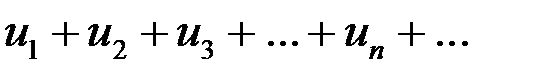(8.2)
и
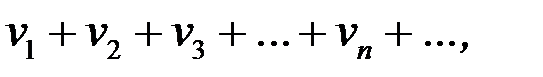(8.3)
все члены которых положительны. Тогда:
1) если члены ряда (8.2) не больше соответствующих членов ряда (8.3), то есть
(
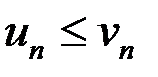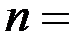1, 2, …), (8.4)
и ряд (8.3) сходится, то сходится и ряд (8.2);
2) если члены ряда (8.2) не меньше соответствующих членов ряда (8.3), то есть
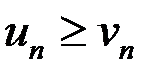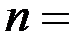( 1, 2, …), (8.5)
и ряд (13.3) расходится, то и ряд (8.2) расходится.
Замечание 8.2. Последняя теорема справедлива и в том случае, когда члены рядов (8.2), (8.3) являются неотрицательными числами, а также в случаях, когда неравенства (8.4) или (8.5) выполняются лишь для 
а не для всех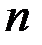 
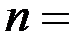( 1, 2, …).
Теорема 8.5. (предельный признак сравнения). Пусть заданы ряды (8.2), (8.3), все члены которых положительны. Если существует конечный и отличный от нуля предел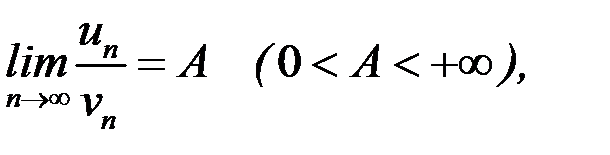 
то ряды 83.2), 83.3) либо оба сходятся, либо оба расходятся.
Замечание 8.3. При применении двух последних теорем по исследуемому ряду (8.2) нужно выбрать самим ряд (8.3) с известным поведением (его называют эталонным рядом). В качестве эталонного ряда чаще всего используют один из двух рядов:
|
|
|
а) ряд Дирихле (обобщенный гармонический ряд)
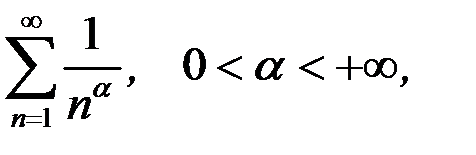
который при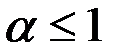 
расходится, а при 
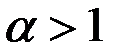сходится;
б) ряд геометрической прогрессии
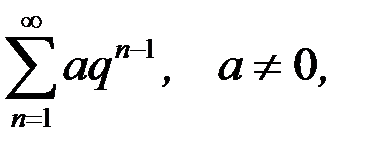
который при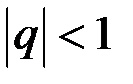 
сходится, а при 
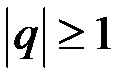расходится.
Признак Даламбера
Пусть все члены ряда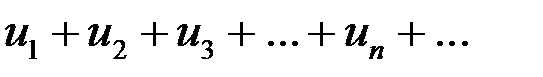 
положительны и существует конечный предел
Тогда ряд сходится при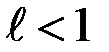 
и расходится при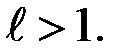 
Замечания к признаку Даламбера:
1) ряд будет расходиться и в том случае, если 
2) если 
то признак Даламбера не дает ответа на вопрос о сходимости ряда (ряд может оказаться как сходящимся, так и расходящимся).
Радикальный признак Коши
Пусть все члены ряда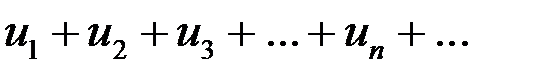 
положительны и существует конечный предел
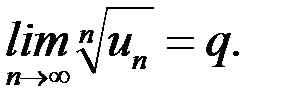
Тогда ряд сходится при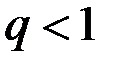 
и расходится при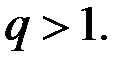 
Замечания к радикальному признаку Коши:
1) ряд будет расходиться и в том случае, если 
2) если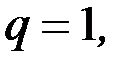 
то радикальный признак Коши не дает ответа на вопрос о сходимости ряда.
