Площадь плоской фигуры

Рассмотрим на плоскости  фигуру, ограниченную графиком непрерывной и положительной функции 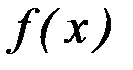, осью  и вертикальными прямыми  и  (рис 6.2). Такая фигура называется криволинейной трапецией.

 

 

Рис. 6.2

 

Площадь криволинейной трапеции равна определенному интегралу от функции 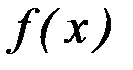  на отрезке :

.

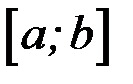Отметим, что если криволинейная трапеция расположена «ниже» оси  (), то ее площадь может находиться по формулам

или .

Если фигура ограничена кривыми 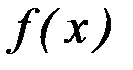 и  (где ), прямыми  и  (см. рис. 5.3), то площадь криволинейной трапеции находится по формуле

.

 

 

Рис. 6.3

 

Объем тела вращения

Пусть вокруг оси  вращается криволинейная трапеция, ограниченная непрерывной линией , осью  и прямыми  и  (см. рис. 5.4). Объем тела вращения определяется формулой

.

Если тело образовано вращением криволинейной трапеции вокруг оси , то выражая  через  как обратную функцию, получаем аналогичную формулу для объема тела вращения:

,

где  – область изменения функции .

 

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

Уравнения, связывающие независимую переменную, искомую функцию и ее производные называются дифференциальными уравнениями (ДУ) (термин принадлежит Г. Лейбницу, 1676 г.).

Решением дифференциального уравнения называется функция, которая при подстановке в уравнение обращает его в тождество. Так, решением уравнения  является функция  – первообразная для функции .

Если искомая (неизвестная) функция зависит от одной переменной, то ДУ называют обыкновенным; в противном случае – ДУ в частных производных. В данном учебном пособии будут рассматриваться только обыкновенные ДУ.

Наивысший порядок производной, входящей в ДУ, называется порядком этого уравнения.

Например, уравнение  – обыкновенное ДУ третьего порядка, а уравнение  – первого порядка;  – ДУ в частных производных первого порядка.

Процесс отыскания решения ДУ называется его интегрированием, а график решения ДУ – интегральной кривой.