2020-10-09
126
Дифференциальное уравнение первого порядка в общем случае можно записать в виде
. (7.1)
Если уравнение (7.1) можно разрешить относительно 
, то его записывают в виде
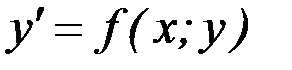(7.2)
и называют ДУ первого порядка, разрешенным относительно производной.
ДУ первого порядка, разрешенное относительно производной, можно записать в дифференциальной форме:
,
где 
и 
– известные функции.
Общим решением ДУ первого порядка называется функция 
, содержащая одну произвольную постоянную и удовлетворяющая условиям:
1) Функция 
является решением ДУ при каждом фиксированном значении 
.
2) каково бы ни было начальное условие 
при 
(записывается в виде 
или 
), можно найти такое значение постоянной 
, что функция 
удовлетворяет данному начальному условию.
Частным решением ДУ первого порядка называется любая функция , полученная из общего решения при конкретном значении постоянной .
Если общее решение ДУ найдено в неявном виде, т.е. в виде уравнения 
, то такое решение называется общим интегралом ДУ. Уравнение 
в этом случае называется частным интегралом уравнения.
Задача отыскания решения ДУ первого порядка, удовлетворяющего заданному начальному условию, называется задачей Коши.
Уравнения с разделяющимися переменными
ДУ с разделяющимися переменными имеют вид
. (7.3)
Особенность уравнения (12.3) в том, что коэффициенты при 
и 
представляют собой произведения функций, одна из которых зависит только от 
, другая – только от 
.
Почленно разделив это уравнение на 
, получаем уравнение с разделенными переменными
, проинтегрировав которое, находим 
– общий интеграл.
Замечание. Уравнение 
также сводится к уравнению с разделенными переменными. Для этого достаточно положить 
и разделить переменные.
