2020-10-09
142
Пусть функция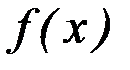 
определена в некоторой окрестности точки 
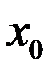и имеет в этой точке производные всех порядков. Тогда ряд
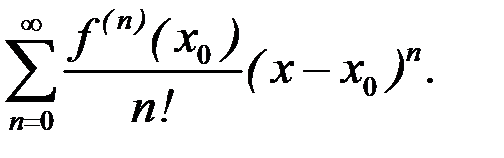(8.14)
называется рядом Тейлора для функции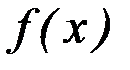
Если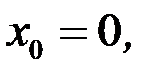 
то ряд (8.14) называется рядом Маклорена для функции 
Если заданная функция 
представлена в виде суммы ряда Тейлора (8.14), то говорят, что функция разложена в ряд Тейлора. В этом случае записывают:
При этом указывают числовой промежуток, на котором имеет место данное разложение.
Известны следующие стандартные разложения элементарных функций в ряды Маклорена:
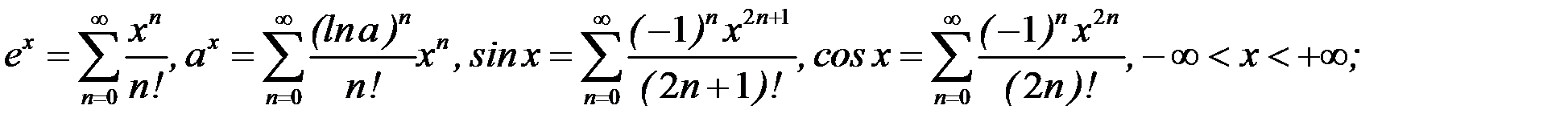
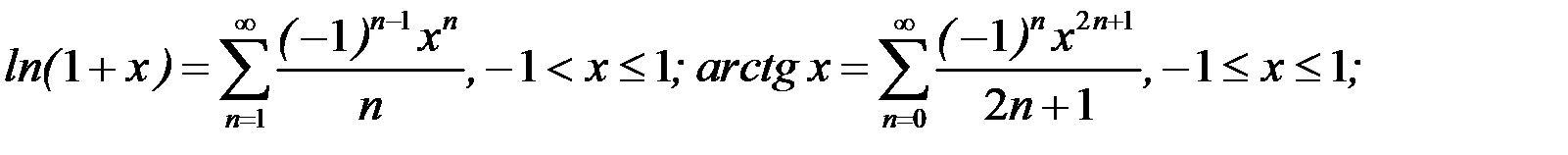
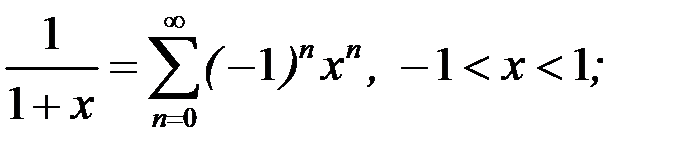
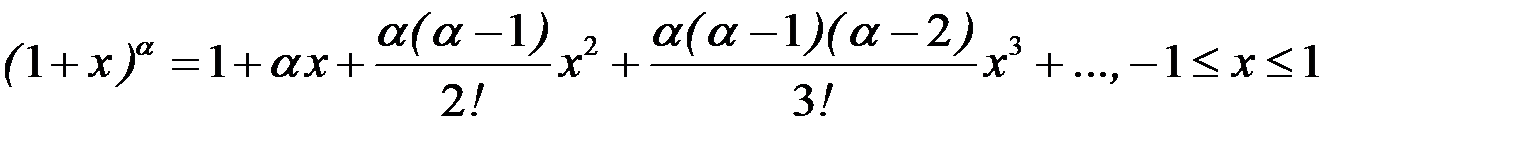при
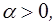
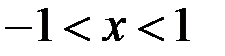при 
при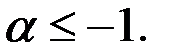 
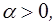
Здесь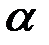 
– любое действительное число, отличное от 0 и от всех натуральных чисел (при натуральном 
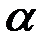получается известное конечное разложение по формуле бинома Ньютона, которое имеет место на промежутке (
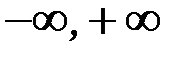)). Последний ряд называется биномиальным.
Заметим, что предпоследнее разложение получается из последнего при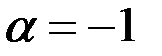 
.
С помощью стандартных разложений можно получать разложения в степенные ряды некоторых сложных функций. Например,
|
|
|
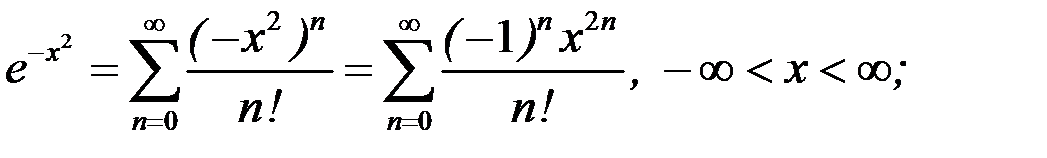
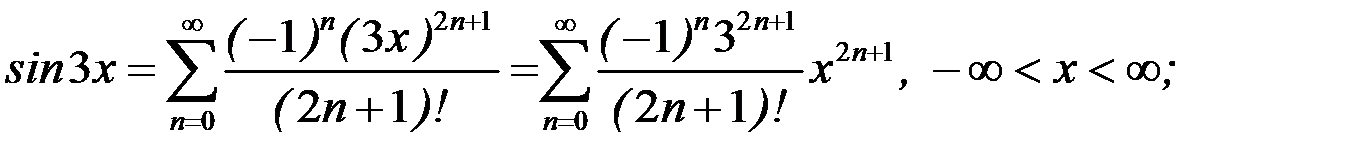
Ряды Тейлора применяют для вычисления значений функций, для вычисления определенных интегралов в тех случаях, когда первообразная подынтегральной функции не выражается в конечном виде через элементарные функции. Ряды Тейлора применяют также при нахождении решений дифференциальных уравнений.
Вопросы для контроля
1.Функция.
2. Область ее определения функции.
3. График функции.
4. Сложные и обратные функции.
5. Основные элементарные функции, их свойства и графики.
6.Числовые последовательности.
7. Предел числовой последовательности.
8. Критерий Коши сходимости числовой последовательности.
9.Арифметические свойства пределов.
10. Переход к пределу в неравенствах.
11. Существование предела монотонной ограниченной последовательности.
12. Предел функции в точке и на бесконечности.
13.Бесконечно малые функции.
14.Бесконечно большие функции.
15. Свойства предела функции.
16. Односторонние пределы.
17. Пределы монотонных функций.
18. Первый замечательный предел.
19. Второй замечательный предел.
20. Непрерывность функции в точке.
21.Локальные свойства непрерывных функций.
22. Непрерывность сложной и обратной функции.
23. Непрерывность элементарных функций.
24.Точки разрыва и их классификация.
25. Свойства функций непрерывных на отрезке: ограниченность, существование наибольшего и наименьшего значений, промежуточные значения.
26.Теорема об обратной функции.
27.Понятие функции дифференцируемой в точке.
28. Производная функции, ее смысл в различных задачах.
29.Правила нахождения производной.
|
|
|
30. Производная сложной и обратной функции.
31. Правила дифференцирования.
32.Точки экстремума функции.
33.Теорема Ферма о необходимом условии экстремума.
34.Теоремы и формула Ролля, Лагранжа, Коши о промежуточных значениях, их применение.
35. Правило Лопиталя.
36.Производные и дифференциалы высших порядков.
37. Условия монотонности функции. Экстремумы функции.
38.Достаточные условия экстремума.
39.Отыскание наибольшего и наименьшего значений функции, дифференцируемой на отрезке.
40. Выпуклость. Точки перегиба.
41. Асимптоты графика функции.
42. Общая схема исследования функции и построения ее графика.
43. Первообразная.
44. Неопределенный интеграл и его свойства.
45. Табличные интегралы.
46. Замена переменной и интегрирование по частям в неопределенном интеграле.
47. Разложение рациональных дробей на простейшие.
48. Задачи, приводящие к понятию определенного интеграла.
49. Определенный интеграл Римана, его свойства.
50. Интегральная сумма.
51. Формула Ньютона-Лейбница, ее применение для вычисления определенных интегралов.
52. Геометрические и механические приложения определенного интеграла.
53. Функции нескольких переменных.
54. Область определения функции нескольких переменных.
55. Предел и непрерывность функции нескольких переменных.
56. Частные производные.
57. Дифференциал функции нескольких переменных, его связь с частными производными.
58. Экстремумы функций нескольких переменных.
59. Необходимое условие экстремума.
60. Достаточное условие экстремума функции нескольких переменных.
61. Условный экстремум, метод множителей Лагранжа.
62. Числовые ряды.
63.Сходимость и сумма ряда.
64. Необходимое условие сходимости.
65. Действия с рядами.
66. Ряды с неотрицательными членами.
67. Признаки сходимости (сравнения, Даламбера, Коши).
68. Знакопеременные ряды.
69. Абсолютная и условная сходимости.
70. Признак Лейбница.
71. Свойства абсолютно сходящихся рядов.
72. Функциональные ряды.
73. Интегрирование и дифференцирование функционального ряда.
74. Степенные ряды.
75. Радиус сходимости. Область сходимости степенного ряда.
76. Теорема Абеля.
77. Непрерывность суммы ряда.
78. Почленное дифференцирование и интегрирование.
79. Ряд Тейлора.
80. Ряд Маклорена
81. Разложение функций в степенные ряды.
