Как уже упоминалось в 1.2.1, такой анализ заключается в выявлении связи распределения значений выходного параметра с действующими на объект испытаний факторами, ее формы, направления, степени влияния.
Общее выражение для коэффициента корреляции из (1) можно представить как:
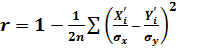 (15)
(15)
где п — количество значений выходного параметра;
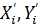 — координаты точки замера относительно осей, проведенных через центр распределения:
— координаты точки замера относительно осей, проведенных через центр распределения:
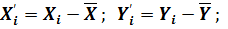
Форма связи может быть определена с помощью уравнений регрессии или эмпирических формул [22].
РЕГРЕССИОННЫЕ МОДЕЛИ
Нормальные уравнения регрессии составляются по виду (1.3.4.) в количестве, соответствующему количеству неизвестных коэффициентов bi. Полученная система уравнений решается обычными математическими методами (метод исключения, метод наименьших квадратов — МНК).
Определение эмпирической формулы линейного вида.
Если числовые данные испытаний укладываются графически достаточно близко от проведенной некоторым образом прямой, то можно предположить существующую здесь линейную зависимость:
у=ах+b.
Пример.
При испытаниях на стенде системы управления поворотным соплом двигательной установки ракеты [4] были получены данные, определяющие зависимость усилия на штоке рулевой машинки (Р) от перепада давления между двигательным отсеком и средой, разделяемых защитной мембраной ( р):
р):
Таблица 5
 р,[кПа] р,[кПа]
| —20,0 | —15,0 | 10,0 | —5,0 | 0 | +5,0 | + 10,0 | + 15,0 | +20 |
| P, [H] | — 101 | —77 | —81 | —57 | —21 | —29 | — 13 | — 11 | + 29 |
На рис. 2 точки расположились сравнительно близко к проведенной прямой. Следовательно, можно считать зависимость P=f( p) линейной.
p) линейной.
Этот же вопрос можно решить аналитически.
Допустим сначала, что точки графика точно удовлетворяют формуле линейной зависимости,
т. е.
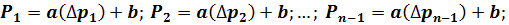
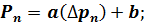
Вычтем из каждого равенства (начиная со второго) предыдущее:
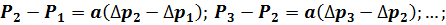
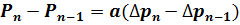 или
или
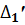 =
= 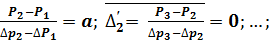
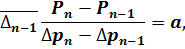
где 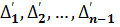 — первые разделенные разности [27];
— первые разделенные разности [27];
i= 1; 2;...; (n-1)
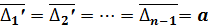 . (34)
. (34)
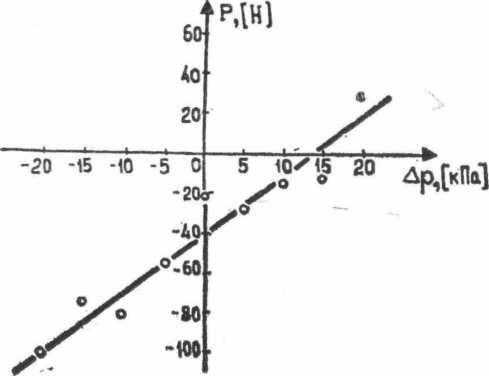
Рис. 2. Экспериментальная зависимость Р = f(  p).
p).
Таким образом, для линейной формулы должно выполняться условие (17). Но при наличии эмпирической формулы (16) равенства (17) будут приближенными, но мало отличающимися (колеблющимися) друг от друга.
По табл. 6 вычислим разности 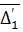 по формулам (16).
по формулам (16).
Из табл. 6 видно, что разности 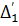 колеблются в сравнительно небольших пределах от +8,0 до —1,6, исключая выпадающее значение
колеблются в сравнительно небольших пределах от +8,0 до —1,6, исключая выпадающее значение 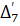 . Следовательно, искомая эмпирическая формула имеет вид линейной зависимости.
. Следовательно, искомая эмпирическая формула имеет вид линейной зависимости.
В нашем примере значения 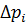 , расположенные в порядке возрастания, образуют арифметическую прогрессию. Обозначим
, расположенные в порядке возрастания, образуют арифметическую прогрессию. Обозначим 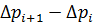 = h — шаг аргумента.
= h — шаг аргумента.
Тогда формула (16) примет вид:
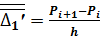 , откуда
, откуда 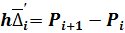 .
.
Таблица 6
| № |  р р
| Р | 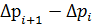
| Pi+1 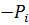
| 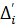
|
| 1. | —20,0 | — 101 | — 15-(—20) = +5,0 | —77—(—101) = +24 | (+ 24): (+5,0) = +4,8 |
| 2. | — 15,0 | —77 | — 10—(—15) = +5,0 | —81—(—77) = —4 | (-4): (+ 5,0) = —0,8 |
| 3. | 10,0 | —81 | —5—(—10) = +5,0 | —57—(-81) = +24 | + 1,8 |
| 4. | —5,0 | —57 | + 5,0 | —21 —(—57) = +36 | + 7,2 |
| 5. | 0 | —21 | + 5,0 | —29— (—21) = —8 | —1,6 |
| 6. | +5,0 | —29 | + 5,0 | — 13—(—29) = +16 | + 3,2 |
| 7. | +10,0 | — 13 | + 5,0 | — 11—(—13) = +2 | +0,4 |
| 8. | +15,0 | — 11 | + 5,0 | +29—(—11) = +40 | + 8,0 |
| 9. | +20,0 | +29 |
| ||
Обозначим 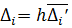 и получим
и получим
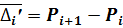 (18)
(18)
Величины 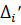 называются первыми неразделенными разностями. Условие (17) перепишем:
называются первыми неразделенными разностями. Условие (17) перепишем:
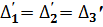 =…=
=…= 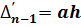 . (19)
. (19)
Т. е. первые неразделенные разности должны мало отличаться друг от друга, что мы отмечаем в табл. 6.
В результате подстановки значении переменных  р и Р в уравнении линейной зависимости появляются уклонения:
р и Р в уравнении линейной зависимости появляются уклонения:
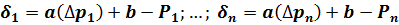 .
.
Используя МНК, находим такие значения параметров а и b, при которых сумма квадратов уклонений была бы минимальной, т. е.:
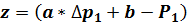 2+
2+ 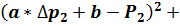
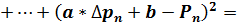 min. (20)
min. (20)
Для этого определим частные производные
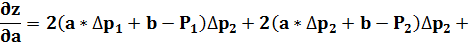
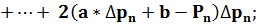
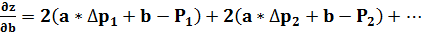
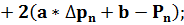
Приравняв частные производные нулю, получим нормальные уравнения:
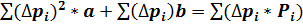 ;
;
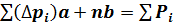 . (21)
. (21)
Следует убедиться в том, что уравнения (21) определят значения параметров при минимуме функции (20). Для этого берем частные производные 2-го порядка:
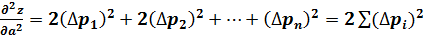 ;
;
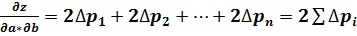 ; (22)
; (22)
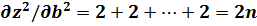
и составляем дискриминант (определитель) D:
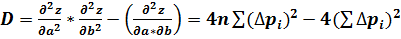 =
= 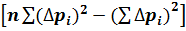
или D > 0 тогда, когда
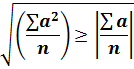
или n 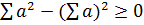
Выведенная разность не может равняться нулю, поскольку определитель системы (22)
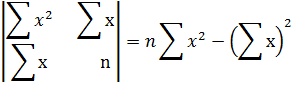
отличен от нуля, т. к. система имеет решение.
Следовательно, D>0 и 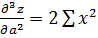 >0, что указывает на наличие минимума функции (37).
>0, что указывает на наличие минимума функции (37).
Проведем расчет параметров а и b методом МНК согласно формулам (22) по данным из табл. 7.
Таблица 7
| № |  р, [кПа] р, [кПа]
| P,[H] |  р2 р2
| Р.  р р
| Р | 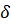
| 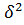
|
| 1. | —20,0 | —101 | + 400,00 | + 2020.0 | —98,9 | + 2,1 | + 4,41 |
| 2. | — 5,0 | —77 | + 225,00 | + 1155.0 | —84,2 | —7,2 | +50.9 |
| 3. | —10,0 | —81 | + 100,00 | + 810,0 | —69,5 | + 11,5 | + 132,1 |
| 4. | —5,0 | —57 | + 25,00 | +285,0 | —54,8 | +2,2 | + 4,84 |
| 5. | 0 | —21 | 0 | 0 | —40,1 | — 19.1 | +366,4 |
| 6. | + 5,0 | —29 | + 25.00 | — 145.0 | —25,4 | + 3.6 | + 10,29 |
| 7 | + 10,0 | — 13 | + 100.00 | — 130.0 | — 10,7 | + 2,3 | + 5,29 |
| 8. | + 15.0 | — 11 | + 225.00 | — 165.0 | + 4,0 | + 15,0 | +225 |
| 9. | + 20,0 | + 29 | + 400,00 | +580,0 | + 18,7 | — 10.3 | + 103.1 |
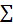
| 0 | —361 | + 1500,00 | + 4410,0 | —360,9 | + 0,1 | + 902,03 |
Нормальные уравнения по данным табл. 7 будут иметь вид:
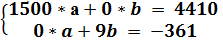
Откуда
a= 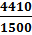 =-2,94; b=-
=-2,94; b=- 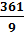 ≈-40,1
≈-40,1
Таким образом, искомая эмпирическая формула будет:
Р = 2,94∆р —40,1.
Подставим сюда значения ∆р для определения значении 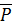 в таблице 11, затем рассчитаем уклонения
в таблице 11, затем рассчитаем уклонения 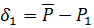 . Здесь сумма квадратов уклонений будет минимальная, причем
. Здесь сумма квадратов уклонений будет минимальная, причем 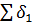 = 0 (в табл. 11
= 0 (в табл. 11 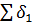 = 0,1, что объясняется округлениями), т. к. сумма равенств, определяющих уклонение:
= 0,1, что объясняется округлениями), т. к. сумма равенств, определяющих уклонение:
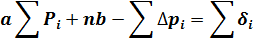
Но левая часть уравнения совпадает с левой частью второго нормального уравнения (21) после переноса 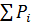 . Определение эмпирических формул, приводящихся к параболическому виду. В этом случае экспериментальные данные должны удовлетворять формуле (или могут быть средние значения функции отклика из плана однофакторного эксперимента или двухфакторного при постоянном значении одного из факторов):
. Определение эмпирических формул, приводящихся к параболическому виду. В этом случае экспериментальные данные должны удовлетворять формуле (или могут быть средние значения функции отклика из плана однофакторного эксперимента или двухфакторного при постоянном значении одного из факторов):
у = а 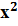 + bх + с. (23)
+ bх + с. (23)
При определении параметров параболической формулы методом МНК используется система нормальных уравнений, выведенных из условия 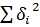 = min:
= min:
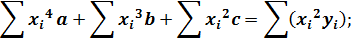
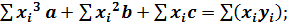 (24)
(24)
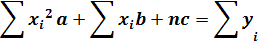
Эмпирические формулы, приводящиеся к линейном виду.
Расчет подобных формул производится, если не выполняются условия принадлежности исследуемых характеристик к линейной или параболической.
Рассмотрим 6 формул, наиболее часто встречаемых в формализованных описаниях процессов испытаний (см. 1.4.2).
Для каждой формулы установим свойство, которому удовлетворяют два крайних значения зависимой переменной (т. е. 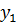 и
и 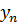 ) и некоторое промежуточное значение
) и некоторое промежуточное значение 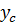 .
.
1. у = аlgx+b (25)
Подставим крайние значения 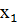 и
и 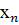 аргумента
аргумента
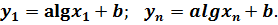
Возьмем среднее геометрическое из двух крайних значений аргумента
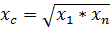 , этому значению будет соответствовать следующее значение зависимой переменной
, этому значению будет соответствовать следующее значение зависимой переменной
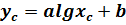
или
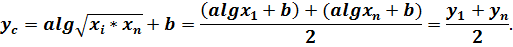
Итак, для функции (25) должно выполняться условие
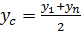 где
где 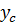 — значение функции при
— значение функции при 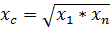 .
.
2. у = а 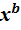 .
.
Также, как и в предыдущем случае, подставляем крайние значения переменных
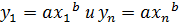 ;
; 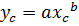
или 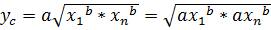 , откуда
, откуда 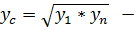 это есть условие, которому удовлетворяет рассматриваемая формула.
это есть условие, которому удовлетворяет рассматриваемая формула.
3. у = а 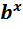 .
.
Подстановка крайних значений дает:
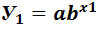 ,
, 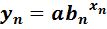 .
.
Берем среднее арифметическое аргумента:
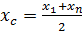 , для которого
, для которого 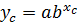 или
или 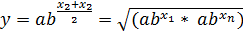 , откуда
, откуда 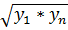 — свойство функции у = а
— свойство функции у = а 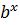 .
.
Сводные данные по аналогичным расчетам для других формул приведены в табл. 8.
Вид эмпирической формулы выбираем, пользуясь таблицей 8. По данным измерений 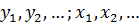 находим
находим 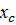 и
и 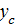 . Затем для этого же значения
. Затем для этого же значения 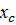 определим
определим 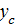 , используя данные испытаний. Если
, используя данные испытаний. Если 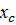 будет равно какому-нибудь
будет равно какому-нибудь 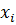 , то
, то 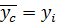 .
.
Таблица 8
| № формулы | 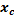
| 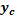
| Формула |
| 1. | 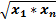
| 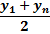
| 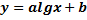
|
| 2. | 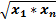
| 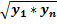
| 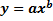
|
| 3 | 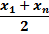
| 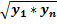
| 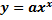
|
| 4. | 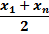
| 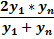
| 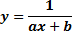
|
| 5. | 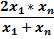
| 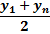
| y-a+ 
|
| 6. | 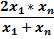
| 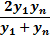
| 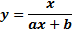
|
Причем xi соответствует 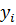 ;
; 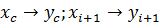 откуда,
откуда,
применяя линейную интерполяцию,
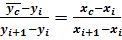 (26)
(26)
Таким образом, для 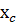 получим 2 значения функции
получим 2 значения функции 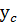 и
и 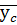 . Если они мало отличаются друг от друга, то выбранная формула подтверждается, в противном случае нужно испытывать следующую за исследованной формулу таблицы 8. Из испытанных формул выбирается та, для которой разность (
. Если они мало отличаются друг от друга, то выбранная формула подтверждается, в противном случае нужно испытывать следующую за исследованной формулу таблицы 8. Из испытанных формул выбирается та, для которой разность (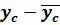 ) будет меньше.
) будет меньше.
Вид зависимостей и их параметры можно определить по формулам, выведенным по МНК, из приложения 3 к ГОСТ 16.305—74.
Пример.
Определить вид эмпирической формулы, выражающей зависимость между усилием на штоке рулевой машинки Р и углом отклонения а поворотного сопла двигательной установки летательного аппарата по эмпирическим данным в таблице 9.
Таблица 9
| Р, [Н] | +500 | +74 | +95 | + 34 | +22 | +6 | -148 | -138 | -178 | -141 | -607 |
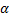 ,[град] ,[град]
| — 10 | —8 | —6 | —4 | —2 | 0 | +2 | +4 | +6 | +8 | +10 |
| № | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
По виду экспериментальной кривой на рис. 3 можно предположить, что мы получили график степенной функции типа 2 (см. табл. 8), т. е.
у = — а 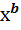 или Р = —a
или Р = —a 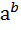
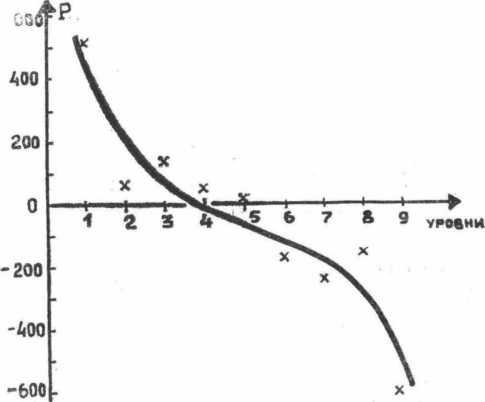
Рис. 3. Экспериментальная зависимость Р = f( 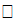 ).
).
По предложенной выше методике определяем: 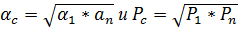 . Поскольку график экспериментальной кривой расположен во 2 и 4 квадрантах, а определение параметров а и b связано с вычислением логарифмов, поэтому мы условно отразим обе ветви графика в 1-ый квадрант и проведем все расчеты для функции Р=+a
. Поскольку график экспериментальной кривой расположен во 2 и 4 квадрантах, а определение параметров а и b связано с вычислением логарифмов, поэтому мы условно отразим обе ветви графика в 1-ый квадрант и проведем все расчеты для функции Р=+a 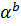 При этом нужно учесть для удобства расчетов смещение графика по ординате на +6 при
При этом нужно учесть для удобства расчетов смещение графика по ординате на +6 при 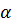 = 0, вычтя 6 из взятых значений функции (см. табл. 10).
= 0, вычтя 6 из взятых значений функции (см. табл. 10).
Таблица 10
| Ветвь из 4-го квадранта | Р | 613 | 147 | 184 | 144 | 154 | 0 |
| Ветвь из 2-го квадранта | Р | 494 | 68 89 | 28 | 16 | 0 |
|
| 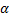
| 10 | 8 6 | 4 | 2 | 0 |
| № | 1 | 2 3 | 4 | 5 | 6 |
Тогда 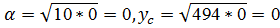 , откуда при
, откуда при 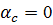 в табл. 10
в табл. 10 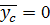 , т.е.
, т.е. 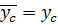 а cледовательно выбор формулы сделан верно.
а cледовательно выбор формулы сделан верно.
Расчеты параметров а и b проведем по формулам, выведенным при помощи МНК (ГОСТ 16.305—74)
6 6 6
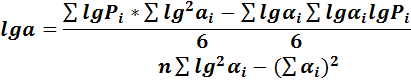
6 6 6
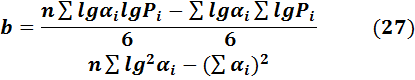
Для удобства можно составить таблицу почленного расчета формул. Окончательно:
lgα= 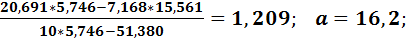
b= 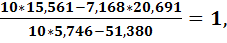
Получили следующее аналитическое выражение экспериментальной зависимости (Р—b)= — 16,2* 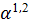 . Для первого приближения такое выражение достаточно адекватно отражает зависимость P=f(a) за исключением концов графика. Последнее говорит о более сложной зависимости типа у =
. Для первого приближения такое выражение достаточно адекватно отражает зависимость P=f(a) за исключением концов графика. Последнее говорит о более сложной зависимости типа у = 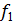 (x)*
(x)* 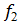 (x) и о проведении дополнительных расчетов либо по усложненной эмпирической формуле, либо по системе нормальных уравнений. В нашей работе ограничимся первой моделью.
(x) и о проведении дополнительных расчетов либо по усложненной эмпирической формуле, либо по системе нормальных уравнений. В нашей работе ограничимся первой моделью.
 2020-10-11
2020-10-11 183
183








