Фононы (нормальные гармонические колебания решетки) квазичастицы, описываемые квантовой статистикой Бозе-Эйнштейна (целый спин или 0). 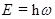 .
.
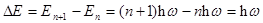 ; D n = ± 1
; D n = ± 1
Для данной частоты wk интервалы одинаковы и равны 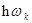 .
.
Фазовое пространство квантовано с размером минимальной ячейки h 3 (D px D x ~ h, D E D t ~ 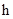 ). Энергия фононов зависит от их частоты w и квантовых чисел n фононных состояний. В состоянии теплового равновесия при Т средние значения квантовых чисел < n > или числа фононов даются формулой Планка для одной фазовой ячейки:
). Энергия фононов зависит от их частоты w и квантовых чисел n фононных состояний. В состоянии теплового равновесия при Т средние значения квантовых чисел < n > или числа фононов даются формулой Планка для одной фазовой ячейки:
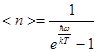 (5.36)
(5.36)
Чтобы вывести эту формулу, учтем распределение осцилляторов в состоянии теплового равновесия по разным соседним состояним (n + 1) и n: так как 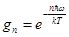 – вероятность состояния n, фактор Больцмана:
– вероятность состояния n, фактор Больцмана:
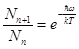 (5.37)
(5.37)
Отношение числа осцилляторов в n -ом состоянии к общему числу всех осцилляторов в твердом теле:
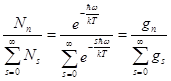 (5.38)
(5.38)
Cреднее значение квантового числа < n > в возбужденном состоянии s:
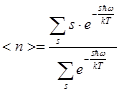 (5.39)
(5.39)
Это среднее число фононов с частотой w (число заполнений данной моды w).
В знаменателе стоит сумма членов бесконечной геометрической прогрессии:
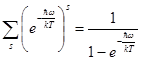 (5.40)
(5.40)
В числителе:
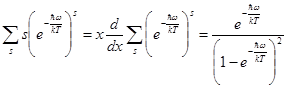 (5.41)
(5.41)
Тогда
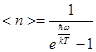 (5.42)
(5.42)
Это и есть формула Планка (5.36), при этом:
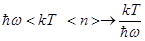 , высокие температуры
, высокие температуры
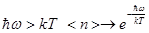 , низкие температуры
, низкие температуры
Средняя энергия осциллятора с частотой w:
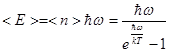 (5.43)
(5.43)
Энергия набора осцилляторов с различными частотами wk:
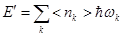 (5.44)
(5.44)
при малых 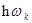 сумма переходит в интеграл.
сумма переходит в интеграл.
Тогда полная энергия фононов в кристалле:
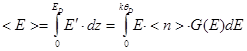 , (5.45)
, (5.45)
где 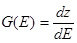 – плотность состояний. (5.46)
– плотность состояний. (5.46)
Плотность состояний G (E) численно равна числу состояний dz в единичном интервале dE = 1.
Для шара 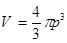 ;
; 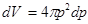
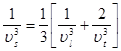
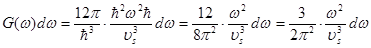
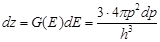 (три поляризации фононов) (5.47)
(три поляризации фононов) (5.47)
Так как
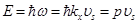 , (5.48)
, (5.48)
подставляя Е в (5.47):
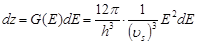 (5.49)
(5.49)
Полное число состояний в кристалле:
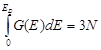
Подставляя (5.49) в (5.45), с учетом (5.42) получим среднюю энергию фононов в кристалле:
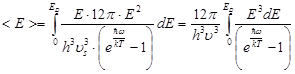 (5.50)
(5.50)
Краткие выводы
1) В трехмерной кристаллической решетке существует 3 SN волн, из которых три волны акустические и (3 S – 3) – оптические.
2) Cобственные колебания атомов кристаллической решетки можно описать с помощью квазичастиц – фононов, которые подчиняются статистике Бозе-Эйнштейна.
3) Среднее число фононов с частотой w описывается формулой Планка 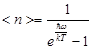 , а средняя энергия осцилляторов с частотой w:
, а средняя энергия осцилляторов с частотой w:
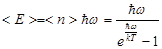 .
.
 2020-10-10
2020-10-10 501
501







