Сместим из равновесия атом с номером n на расстояние Un. По цепочке пройдет волна сжатия. Найдем уравнение движения n -го атома. Пусть его смещение Un (x, t) невелико по сравнению с a, т.е. силы со стороны соседей можно считать квазиупругими и согласно закону Гука они пропорциональны смещениям. Действие силы Гука уравновешивается обычной силой Ньютона. Учтем только ближайшие атомы:
 (5.8)
(5.8)
Соответствующее уравнение движения:
 (5.9)
(5.9)
Решение (2) ищем в виде бегущей волны:
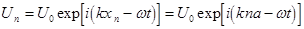 , (5.10)
, (5.10)
где U0 – амплитуда;
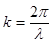 ;
;
w – круговая частота.
Подставив (5.10) в (5.9), имеем:
 , (5.11)
, (5.11)
так как

тогда
 (5.12)
(5.12)
Это периодическая функция, w – четная функция k: w 2(k) = w 2(– k) (рис. 5.4).

Рис. 5.4. Зависимость частоты колебаний w цепочки атомов от волнового вектора 
Из (5.12) следует, что все атомы колеблются с дискретными частотами w, зависящими от 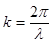 (
(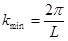 ;
; 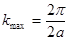 ).
).
 (5.13)
(5.13)
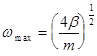 , (5.14)
, (5.14)
с другой стороны w max» 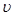 зв × k max =
зв × k max = 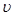 зв ×(p/ a).
зв ×(p/ a).
w max = 5×103 м/с×1010 м–1 @ 5×1013 с–1.
Из рис. 5.5 видно, что короткие волны распространяются медленнее, чем длинные, из-за инерции масс частиц цепочки. Для длинных волн (k мало) фазовая скорость:

 (5.15)
(5.15)
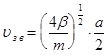
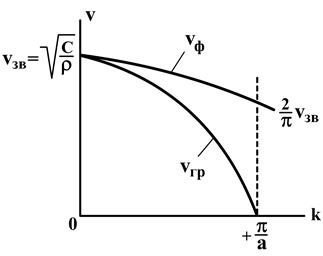
Рис. 5.5. Групповая 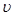 гр и фазовая
гр и фазовая 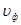 скорости распространения колебаний в цепочке атомов
скорости распространения колебаний в цепочке атомов
Так как скорость звука зависит от l:  (дис-персия), то распространение характеризуется фазовой
(дис-персия), то распространение характеризуется фазовой 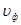 и групповой
и групповой 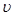 гр скоростями:
гр скоростями:
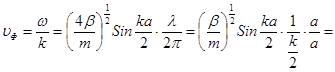
 , (5.16)
, (5.16)
при 

 (5.17)
(5.17)
Фазовая скорость характеризует перемещение фазы колебаний. При малых значениях k: 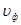 =
= 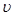 гр =
гр = 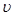 зв.
зв.
Групповая скорость характеризует перемещение вещества или перенос энергии колебаний и при  :
: 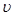 гр = 0, т.е. при этих условиях образуются стоячие волны и энергия не переносится.
гр = 0, т.е. при этих условиях образуются стоячие волны и энергия не переносится.
В бесконечной цепочке трудно определить граничные условия, но такую цепочку можно смоделировать кольцом, таким образом, что последний атом n = N находится на расстоянии a от первого n = 1.
Это периодические граничные условия Борна-Кармана (условия цикличности):
Un+N = Un,
т.е. из (5.10)
 (5.18)
(5.18)
Это справедливо, если exp(ikNa) = 1, или kNa = 2 pn (n = 0, ±1, ±2,...), т.е.
 (5.19)
(5.19)
Таким образом, k – квантуется (N штук) (рис. 5.4).
Границы зоны Бриллюэна: 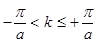 .
.
Зона Бриллюэна – это интервал значений волновых векторов  , содержащий все возможные значения энергии системы, повторяющиеся с периодом
, содержащий все возможные значения энергии системы, повторяющиеся с периодом 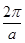 .
.
Число собственных значений k в пределах зоны Бриллюэна равно N – числу атомов или элементарных ячеек в цепочке (число нормальных колебаний).
 2020-10-10
2020-10-10 242
242








