Контрольная работа
«Векторная алгебра»
Если известны координаты точек 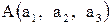 и
и 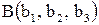 , то координаты вектора
, то координаты вектора 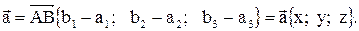
Разложение этого вектора по ортам 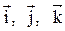 :
: 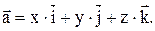
Длина вектора находится по формуле 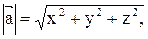 а направляющие косинусы равны
а направляющие косинусы равны 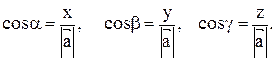 Орт вектора
Орт вектора 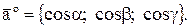
Пример 1. Даны точки 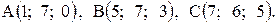
Разложить вектор 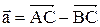 по ортам
по ортам 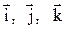 и найти его длину, направляющие косинусы, орт вектора
и найти его длину, направляющие косинусы, орт вектора  . Найдем координаты векторов:
. Найдем координаты векторов:
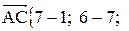
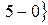
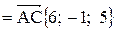 и
и 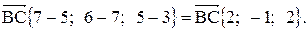
Вектор 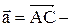
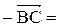
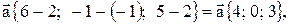

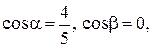
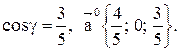
Контрольные варианты к задаче 1. Даны точки А, В и С. Разложить вектор  по ортам
по ортам 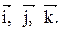 Найти длину, направляющие косинусы и орт вектора
Найти длину, направляющие косинусы и орт вектора  .
.
| 1. | 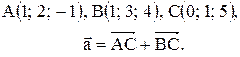
| 2. | 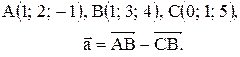
|
| 3. | . 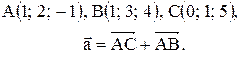
| 4. | 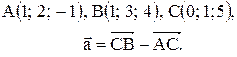
|
| 5. | 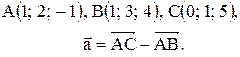
| 6. | 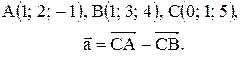
|
| 7. | 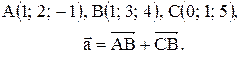
| 8. | 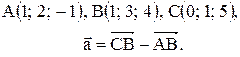
|
| 9. | 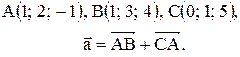
| 10. | 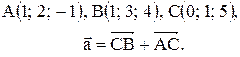
|
| 11. | 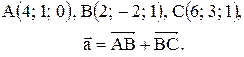
| 12. | 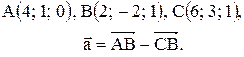
|
| 13. | 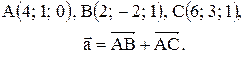
| 14. | 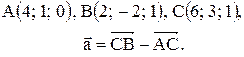
|
| 15. | 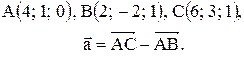
| 16. | 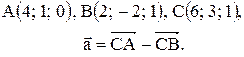
|
| 17. | 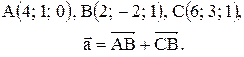
| 18. | 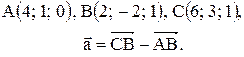
|
| 19. | 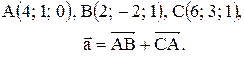
| 20. | 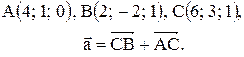
|
| 21. | 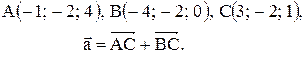
| 22. | 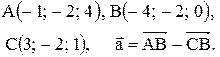
|
| 23. | 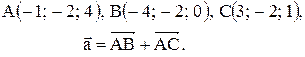
| 24. | 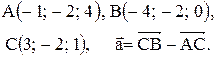
|
| 25. | 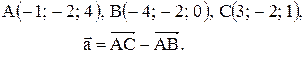
| 26. | 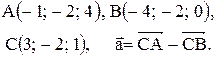
|
| 27. | 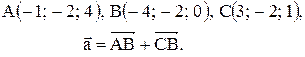
| 28. | 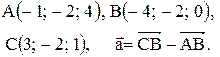
|
| 29. | 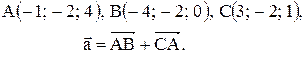
| 30. | 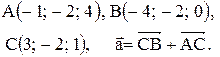
|
Задача 2. Если даны векторы 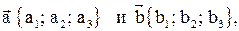 то
то 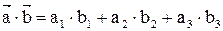 .
.
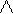 Тогда
Тогда 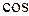
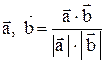 ; проекция вектора
; проекция вектора 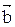 на направление вектора
на направление вектора 
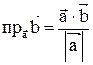 , условие перпендикулярности ненулевых векторов выглядит следующим образом:
, условие перпендикулярности ненулевых векторов выглядит следующим образом: 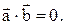
Условие коллинеарности векторов: 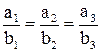 .
.
Пример 2. Даны вершины треугольника 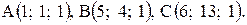 Найти угол при вершине А и проекцию вектора
Найти угол при вершине А и проекцию вектора 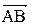 на сторону АС. С
на сторону АС. С
 Внутренний угол при вершине А образован векторами
Внутренний угол при вершине А образован векторами 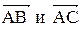 ,
,
 А В
А В
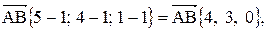
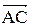
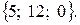
Тогда 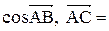
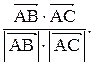
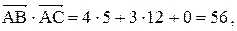
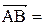
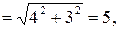
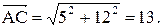
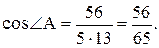
Проекция 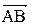 на направление вектора
на направление вектора 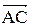 :
: 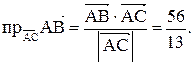
Контрольные варианты к задаче 2
1. Даны векторы 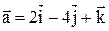 и
и 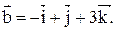 Найти
Найти 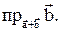
2. Найти косинус угла, образованного вектором 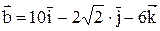 и осью OZ.
и осью OZ.
3. Даны векторы 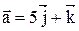 и
и 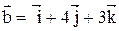 . Найти косинус угла между диагоналями параллелограмма, построенного на векторах
. Найти косинус угла между диагоналями параллелограмма, построенного на векторах 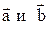 .
.
4. Даны векторы 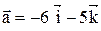 и
и 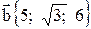 . Вычислить
. Вычислить 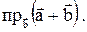
5. Найти косинус угла, образованного вектором 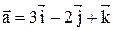 и осью ОУ.
и осью ОУ.
6. Даны векторы 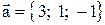 и
и 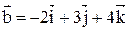 . Найти косинус угла, образованного вектором
. Найти косинус угла, образованного вектором 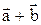 и осью ОХ.
и осью ОХ.
7. Даны векторы 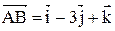 и
и 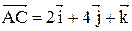 . Найти
. Найти 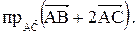
8. Вычислить проекцию вектора 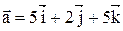 на ось вектора
на ось вектора 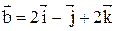 .
.
9. Определить угол между диагоналями параллелограмма, построенного на векторах 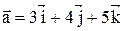 и
и 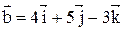 .
.
10. Определить, при каком значении m векторы 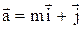 и
и 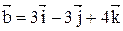 перпендикулярны.
перпендикулярны.
11. Определить, при каком значении 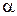 векторы
векторы 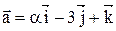 и
и 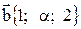 взаимно перпендикулярны.
взаимно перпендикулярны.
12. Даны вершины треугольника: 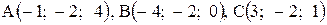 . Определить внутренний угол при вершине В.
. Определить внутренний угол при вершине В.
13. Даны вершины треугольника: 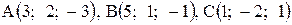 . Определить внутренний угол при вершине А.
. Определить внутренний угол при вершине А.
14. Найти вектор 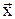 , коллинеарный вектору
, коллинеарный вектору 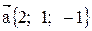 и удовлетворяющий условию
и удовлетворяющий условию 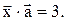
15. Даны две точки 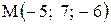 и
и 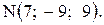 Вычислить проекцию вектора
Вычислить проекцию вектора 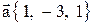 на ось вектора
на ось вектора 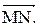
16. Даны векторы: 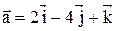 и
и 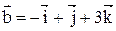 . Вычислить
. Вычислить 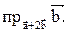
17. Найти острый угол между диагоналями параллелограмма, построенного на векторах 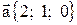 ,
, 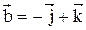 .
.
18. Даны три вектора: 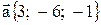 ,
, 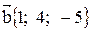 ,
, 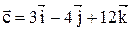 . Найти
. Найти 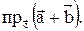
19. Даны три вектора: 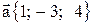 ,
, 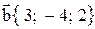 ,
, 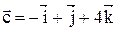 . Найти
. Найти 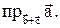
20. Найти острый угол между диагоналями параллелограмма, построенного на векторах 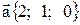 и
и 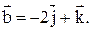
21. Даны три вектора: 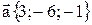 ,
, 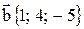 ,
, 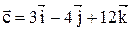 . Вычислить
. Вычислить 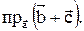
22. Найти вектор 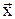 , зная, что он перпендикулярен векторам
, зная, что он перпендикулярен векторам 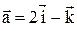 и
и 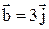
и удовлетворяет условию 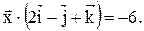
23. Найти вектор 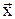 , коллинеарный вектору
, коллинеарный вектору 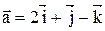 и удовлетворяющий условию
и удовлетворяющий условию 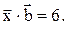
24. Даны вершины треугольника: 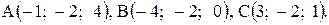 Определить внешний угол при вершине А.
Определить внешний угол при вершине А.
25. Даны вершины треугольника: 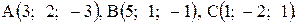 Определить внешний угол при вершине А.
Определить внешний угол при вершине А.
26. Дан вектор 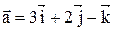 и точки
и точки 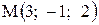 и
и 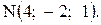 Найти
Найти 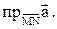
27. В треугольнике с вершинами 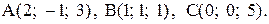 Определить внутренний угол при вершине А.
Определить внутренний угол при вершине А.
28. Даны векторы 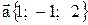 и
и 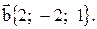 Найти проекцию вектора
Найти проекцию вектора 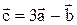 на направление вектора
на направление вектора 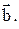
29. Даны вершины треугольника: 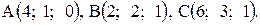 Найти проекцию вектора
Найти проекцию вектора 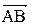 на сторону
на сторону 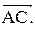
30. Даны векторы 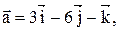
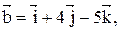
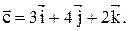 Найти проекцию вектора
Найти проекцию вектора 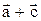 на вектор
на вектор 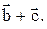
Задача 3. Площадь параллелограмма, построенного на векторах 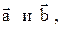
можно найти по формуле 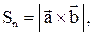 а площадь треугольника, построенного
а площадь треугольника, построенного
на этих векторах: 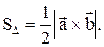
Пример 3. Даны вершины треугольника 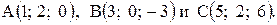 Найти его площадь и длину высоты, опущенной из вершины С.
Найти его площадь и длину высоты, опущенной из вершины С.
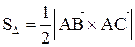 . Находим векторы
. Находим векторы 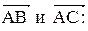
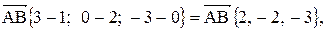
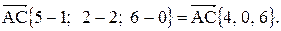
Векторное произведение 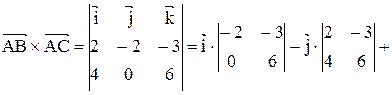
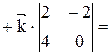
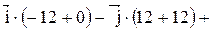
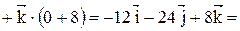
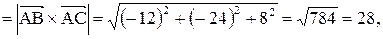
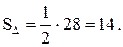
Так как 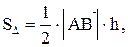 где
где 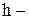 длина высоты, опущенной из вершины С на сторону АВ,
длина высоты, опущенной из вершины С на сторону АВ, 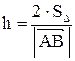 .
. 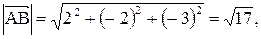
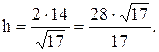
 2020-10-12
2020-10-12 108
108







