Резонансом называют такое состояние пассивной электрической цепи, состоящей из разнохарактерных реактивных элементов, при котором фазовый сдвиг между входным током и входным напряжением равен нулю. При этом входное реактивное сопротивление и/или входная реактивная проводимость цепи равны нулю.
Простейший колебательный контур содержит индуктивный и ёмкостный элементы, соединённые последовательно (последовательный контур)или параллельно (параллельный контур). В последовательном контуре возникает резонанс напряжений, а в параллельном – резонанс токов.
Частоту, на которой наблюдается явление резонанса, называют резонансной.
На рис.10.17 изображена схема последовательного контура, к которому приложено гармоническое напряжение с частотой 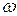 .
.
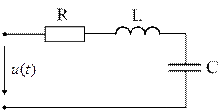
Рис. 10.1
Комплексное входное сопротивление контура на данной частоте
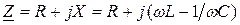 . (10.1)
. (10.1)
При резонансе 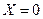 или
или 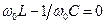 , отсюда получаем уравнение резонансной частоты
, отсюда получаем уравнение резонансной частоты 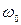 :
: 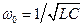 (10.2)
(10.2)
На резонансной частоте сопротивление контура носит чисто резистивный характер, т. е. 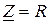 , ток совпадает по фазе с приложенным напряжением и достигает максимального значения
, ток совпадает по фазе с приложенным напряжением и достигает максимального значения 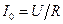 . Сопротивления индуктивности и емкости на резонансной частоте
. Сопротивления индуктивности и емкости на резонансной частоте  равны друг другу:
равны друг другу:
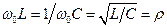 . (10.3)
. (10.3)
Величина 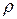 носит название характеристического сопротивления контура.
носит название характеристического сопротивления контура.
Резонансные свойства контура характеризуются его добротностью, которая в общем случае определяется как:
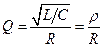 . (10.4)
. (10.4)
Отношение действующих значений напряжений на реактивных элементах (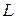 и
и 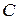 ) к действующему значению приложенного напряжения при резонансе:
) к действующему значению приложенного напряжения при резонансе:
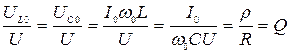 . (10.5)
. (10.5)
Таким образом, добротность 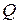 показывает, во сколько раз напряжения на реактивных элементах превышают приложенное напряжение на резонансной частоте.
показывает, во сколько раз напряжения на реактивных элементах превышают приложенное напряжение на резонансной частоте.
На рис. 10.2 изображены зависимости  ,
,  , определяемые формулами:
, определяемые формулами:
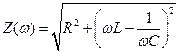 ,
, 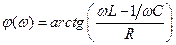 . (10.6)
. (10.6)
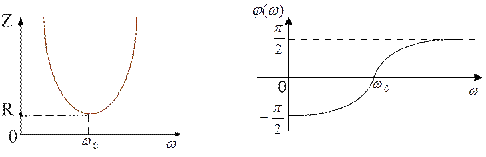
Рис. 10.2
Из представленных характеристик следует, что при 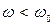 цепь имеет ёмкостный характер
цепь имеет ёмкостный характер 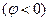 и ток опережает по фазе приложенное напряжение, при
и ток опережает по фазе приложенное напряжение, при 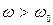 характер цепи индуктивный
характер цепи индуктивный 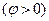 и ток отстаёт по фазе от приложенного напряжения; при
и ток отстаёт по фазе от приложенного напряжения; при 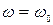 наступает резонанс напряжений
наступает резонанс напряжений 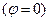 и ток совпадает по фазе с приложенным напряжением. Полное сопротивление цепи принимает при резонансе минимальное значение
и ток совпадает по фазе с приложенным напряжением. Полное сопротивление цепи принимает при резонансе минимальное значение 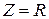 .
.
Зависимость действующего значения тока от частоты определяется уравнением:
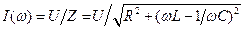 . (10.7)
. (10.7)
Анализ зависимости 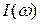 показывает, что она достигает максимума при резонансе
показывает, что она достигает максимума при резонансе 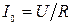 .
.
Степень отклонения частоты воздействия от резонансной частоты принято оценивать абсолютной, относительной и обобщённой расстройками. Расстройки определяются следующим образом:
абсолютная 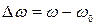 или
или 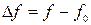 ;
;
относительная 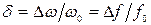 ; (10.8)
; (10.8)
обобщённая 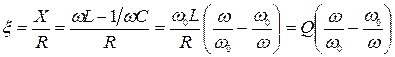 .
.
Важной характеристикой колебательного контура является полоса пропускания. В общем случае абсолютной полосой пропускания называют диапазон частот, в пределах которого резонансная характеристика уменьшается в 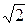 раз по сравнению с ее максимальным значением. Абсолютная полоса пропускания
раз по сравнению с ее максимальным значением. Абсолютная полоса пропускания 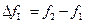 , где
, где 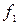 и
и 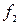 - нижняя и верхняя граничные частоты полосы пропускания:
- нижняя и верхняя граничные частоты полосы пропускания:
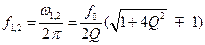 . (10.9)
. (10.9)
Из вышеизложенного следует, что на границе полосы пропускания 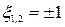 и
и 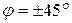 .
.
Абсолютную и относительную полосу пропускания 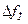 можно выразить через добротность
можно выразить через добротность 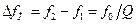 (10.10)
(10.10)
Формула (10.10) показывает, что чем выше добротность 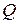 , тем меньше полоса пропускания и наоборот. Следует отметить, что подключение к контуру сопротивления нагрузки приводит к увеличению резистивных потерь контура и, следовательно, к уменьшению его добротности и расширению полосы пропускания.
, тем меньше полоса пропускания и наоборот. Следует отметить, что подключение к контуру сопротивления нагрузки приводит к увеличению резистивных потерь контура и, следовательно, к уменьшению его добротности и расширению полосы пропускания.
Простейший параллельный колебательный контур с потерями в ветвях 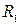 и
и 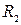 имеет вид, изображённый на рис. 10.3.
имеет вид, изображённый на рис. 10.3.
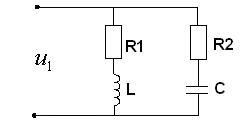
Рис. 10.3
Комплексная входная проводимость такого контура
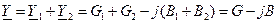 , (10.11)
, (10.11)
где 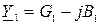 ;
; 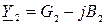 - комплексные проводимости ветвей с индуктивностью и ёмкостью соответственно.
- комплексные проводимости ветвей с индуктивностью и ёмкостью соответственно.
Из условий резонанса токов имеем: 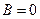 . Отсюда следует:
. Отсюда следует:
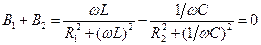 . (10.12)
. (10.12)
Решив (10.12) относительно 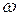 , получим уравнение резонансной частоты:
, получим уравнение резонансной частоты:
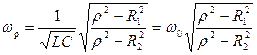 . (10.13)
. (10.13)
Из уравнения (10.13) следует, что резонанс в параллельном контуре возможен лишь в случае, когда подкоренное выражение положительно (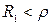 и
и 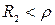 , или
, или 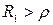 и
и 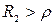 ).
).
Наибольший практический интерес представляет резонанс токов в контурах с малыми потерями. В этом случае уравнение резонансной частоты примет вид (10.2), т.е. совпадает с выражением для последовательного контура. Эквивалентное сопротивление такого контура стремится к бесконечности, и входной ток стремится к нулю. Эквивалентное резонансное сопротивление будет равно
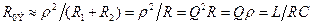 , где
, где 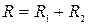 . (10.14)
. (10.14)
Тогда действующие значения токов в ветвях равно
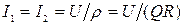 . (10.15)
. (10.15)
Из уравнений (3.76) и (3.78) следует, что отношение токов в ветвях к току в неразветвлённой части цепи на резонансной частоте равно добротности контура:
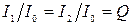 , (10.16)
, (10.16)
т.е. токи в реактивных элементах 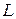 и
и 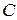 при резонансе в
при резонансе в 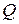 раз больше тока на входе контура. Поэтому в параллельном контуре наблюдается резонанс токов. Резонансная кривая обратно-пропорциональна кривой, изображенной на рис. 10. 2.
раз больше тока на входе контура. Поэтому в параллельном контуре наблюдается резонанс токов. Резонансная кривая обратно-пропорциональна кривой, изображенной на рис. 10. 2.
Лекция 6
 2020-10-12
2020-10-12 179
179








