2020-10-12
134
Рассмотрим таблицу (матрицу) из девяти чисел (элементов матрицы):
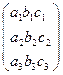(1)
Определение: Определителем третьего порядка, соответствующим матрице (1), называется число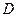 
, равное следующей алгебраической сумме произведений элементов матрицы:
.
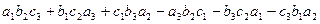Закон составления 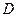оказывается весьма простым, если воспользоваться правилом, которое называется правилом треугольников или правилом Саррюса.
Пример 1.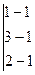 
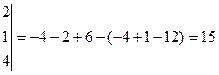
Рассмотрим матрицу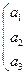 
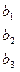
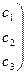и соответствующий ей определитель
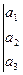
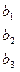
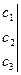
Определение: Минором любого элемента этого определителя называется определитель второго порядка, соответствующий матрице, полученной из данной вычеркиванием строки и столбца, в которых лежит указанный элемент.
Минором элемента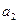 
является определитель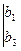 
.
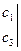Определение: Алгебраическим дополнением любого элемента определителя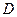 
называют минор этого элемента, взятый со знаком 
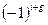, где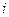 
– номер строки, 
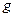– номер столбца определителя 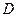, в которых лежит данный элемент.
Обозначают алгебраическое дополнение элемента обычно большой буквой того же наименования и с тем же номером (индексом), что и у данного элемента. Например, алгебраическое дополнение элемента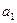 
обозначают 
, 
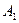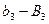и т.д.
|
|
|
Таким образом, по определению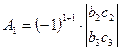 
; 
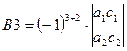и т.д.
Теорема. Определитель 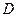равен сумме произведений элементов любого его столбца или строки на их алгебраические дополнения.
Другими словами, имеют место следующие равенства:
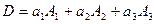
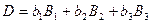
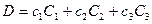
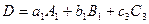
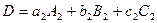
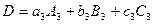
Запись 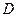по любой из указанных формул называется разложением этого определителя по элементам соответствующего столбца или строки. Эти разложения удобно использовать для вычисления определителей третьего порядка. Для определителей третьего порядка справедливы все свойства 1–7, рассмотренные выше для определителей второго порядка.
Применение определителей
