«Линейная алгебра»
Задание 1.
Даны две матрицы  и
и 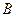 . Найти: а)
. Найти: а) 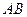 ; б)
; б) 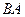 ; в)
; в)  ; г)
; г) 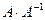 .
.
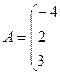
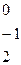
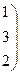
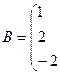
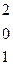
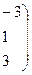
Решение:
а) Произведение 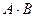 имеет смысл, так как число столбцов матрицы
имеет смысл, так как число столбцов матрицы 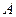 равно числу строк матрицы
равно числу строк матрицы 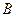 . Находим матрицу
. Находим матрицу 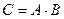 , элементы которой определяются по формуле
, элементы которой определяются по формуле 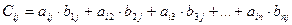
Имеем 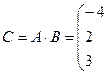
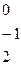
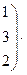
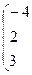
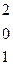
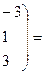
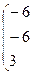

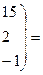
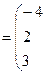
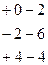
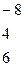
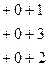
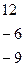
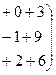
б) Вычислим
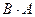
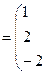
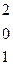
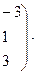
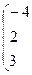
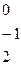
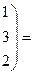

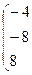
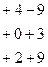
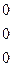
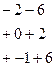

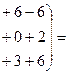
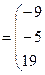
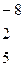
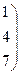
Очевидно, что 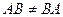 ;
;
в) Матрица 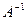 называется обратной по отношению к матрице
называется обратной по отношению к матрице 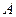 , если
, если 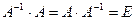 , где
, где 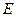 – единичная матрица
– единичная матрица 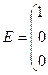

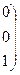
Обратная матрица 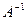 матрицы
матрицы  имеет вид
имеет вид 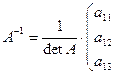
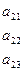
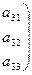 , где
, где
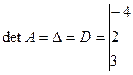
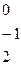
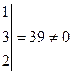 , т.е. матрица невырожденная, и, значит, существует матрица
, т.е. матрица невырожденная, и, значит, существует матрица 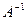 . Находим:
. Находим: 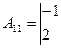
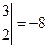 ,
, 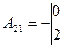
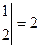 ,
,
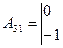
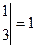 ,
, 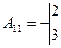
 ,
, 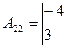
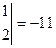 ,
, 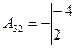
 ,
,
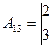
 ,
, 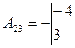
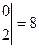 ,
, 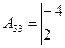
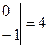 .
.
Тогда
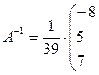


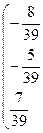

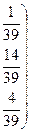
г) Имеем:
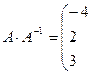
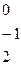
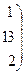
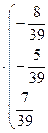

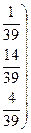 =
= 

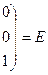
Задание 2.
Проверить совместность линейной системы уравнений и в случае совместности решить её:
а) по формулам Крамера;
б) методом Гауса.

Решение:
Совместность данной системы проверим по теореме Кронекера-Капелли. С помощью элементарных преобразований найдём ранг данной матрицы
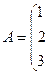
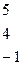
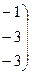 и ранг расширенной матрицы
и ранг расширенной матрицы 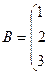
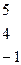
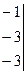
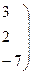 .
.
Для этого умножим первую строку матрицы 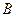 на
на  и сложим со второй, затем умножим первую строку на
и сложим со второй, затем умножим первую строку на 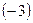 и сложим с третьей, поменяем местами второй и третьи столбцы.
и сложим с третьей, поменяем местами второй и третьи столбцы.
Получим:
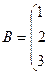
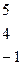
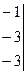
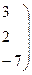 ~
~ 
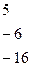

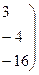 ~
~ 
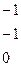
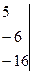
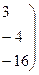 .
.
Следовательно, 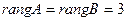 , т.е. числу неизвестных. Значит, исходная система совместна и имеет единственное решение.
, т.е. числу неизвестных. Значит, исходная система совместна и имеет единственное решение.
а) по формулам Крамера
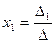 ;
; 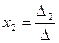 ;
; 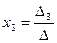
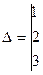
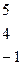
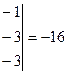 ,
, 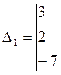
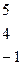
 ,
, 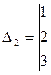
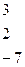
 ,
,

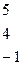
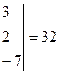 , находим
, находим 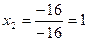 ;
; 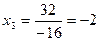 .
.
б) Решим систему методом Гаусса.
Исключим 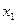 из второго и третьего уравнений. Для этого первое уравнение умножим на
из второго и третьего уравнений. Для этого первое уравнение умножим на  и вычтем из второго, затем первое уравнение умножим на
и вычтем из второго, затем первое уравнение умножим на 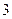 и вычтем из третьего:
и вычтем из третьего: 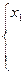
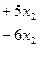
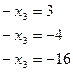
Из полученной системы находим
 ;
;  ;
; 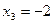
Задание 3.
Проверить совместность линейной системы уравнений и в случае совместности решить её:
а) по формулам Крамера;
б) методом Гаусса.
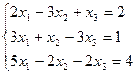
Решение:
Проверяем совместность системы с помощью теоремы Кронекера-Капелли. В расширенной матрице меняем третий и первый столбцы местами, умножаем первую строку на 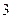 и прибавляем ко второй, умножаем первую строку на
и прибавляем ко второй, умножаем первую строку на  и прибавляем к третьей, из второй строки вычитаем третью:
и прибавляем к третьей, из второй строки вычитаем третью:

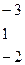

 ~
~ 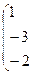
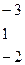
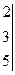
 ~
~ 
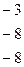

 ~
~ 
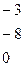

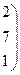
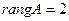 ,
, 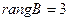 .
.
Согласно теореме Кронекера-Капелли из того, что 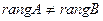 следует несовместность исходной системы.
следует несовместность исходной системы.
Задание 4.
Решить однородную систему линейных алгебраических уравнений.
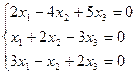
Решение:
Определитель системы 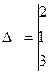
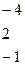
 , поэтому система имеет единственное нулевое решение:
, поэтому система имеет единственное нулевое решение: 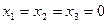
Задание 5.
Решить однородную систему линейных алгебраических уравнений.
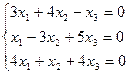
Решение:
Т.к. 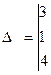
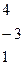
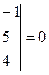 , то система имеет бесчисленное множество решений. Поскольку
, то система имеет бесчисленное множество решений. Поскольку 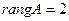 ,
, 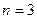 , возьмём любые два уравнения системы (например, 1-е и 2-е) и найдем её решение. Имеем:
, возьмём любые два уравнения системы (например, 1-е и 2-е) и найдем её решение. Имеем:
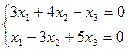
Т.к. определитель из коэффициентов при неизвестных 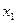 и
и  не равен
не равен 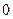 , то в качестве базисных неизвестных возьмём
, то в качестве базисных неизвестных возьмём 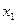 и
и  (хотя можно брать и другие пары неизвестных) и переместим члены с
(хотя можно брать и другие пары неизвестных) и переместим члены с 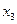 в правые части уравнений:
в правые части уравнений:

Решаем последнюю систему по формулам Крамера:

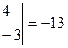 ,
, 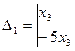
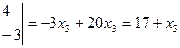 ,
, 
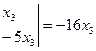 .
.
 2020-10-12
2020-10-12 127
127








