К решению систем линейных уравнений

Рассмотрим систему двух уравнений первой степени (линейных уравнений) с неизвестными и :

(1)

Числа 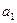, , , 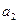называют коэффициентами, а числа , – свободными членами. В случае, если , система (1) называется однородной системой линейных уравнений, в противном случае, т.е. если хотя бы одно из чисел и отлично от нуля, – неоднородной.

Решением системы (1) является всякая пара чисел , , обращающая оба уравнения системы в тождества.

Назовем главным определителем , определитель составленный из коэффициентов при неизвестных , назовем вспомогательными определителями. Если , то система имеет единственное решение. Его можно найти по формулам ; , называемым формулами Крамера.

Пусть , при этом оба определителя и также равны , то в этом случае система имеет бесчисленное множество решений.

Если же , но среди определителей и хотя бы один не равен , то система решений не имеет.

Пример 2. Решить системы уравнений

Найдём . Система имеет единственное решение

По формулам Крамера получаем , .

Пример 3.

, ,

Система имеет бесчисленное множество решений. Решения этой системы – пары чисел , , где – любое число.

Пример 4.

Система решений не имеет, т.к. , .

Пусть дана система трех уравнений первой системы с неизвестными , , :

Числа при неизвестных назовем коэффициентами системы, а числа , , – свободными членами.

Решением системы является всякая тройка чисел , , , обращающая уравнения системы в тождества. Система, имеющая решение, называется совместной.

Если , то система имеет единственное решение. Его можно найти по формулам Крамера: , ,

Здесь – определитель системы

, , – определители, полученные из заменой в нём соответственно первого, второго и третьего столбцов столбцом свободных членов данной системы.

Пример 5. Решите систему уравнений

Вычислим

Т.к. , система имеет единственное решение.

Найдём его по формулам Крамера:

, , , следовательно

, ,

Пример 6. Решите систему уравнений (самостоятельно)

Система несовместна, т.к. ,

Пример 7. Решите систему уравнений (самостоятельно)

Система имеет бесчисленное множество решений

Решение систем линейных уравнений с – неизвестными

Система – линейных уравнений с – неизвестными , , … может быть записана в общем виде так: (1)

Где – коэффициенты, – свободные члены ( – номер строки, – номер столбца). Соответствующий определитель запишем так:

Определение: Минором любого элемента этого определителя называется определитель -го порядка, соответствующий матрице, полученной из данной вычеркиванием строки и столбца, в которых лежит указанный элемент. Минор элемента будем обозначать .

Определение: Алгебраическим дополнением любого элемента определителя называется его минор , взятый со знаком числа .

Алгебраическое дополнение элемента будем обозначать . Таким образом,

Можно доказать теорему: Если определитель системы (1) отличен от нуля, то эта система совместна и определена, причём её единственное решение может быть найдено по формулам Крамера: ; ; …, .

Если же , то система либо не совместна, либо имеет бесчисленное множество решений.

Пример 8. Решить систему уравнений:

Система совместна, т.к.

Вычисляя , , , , получаем:

Следовательно, , , , – решение системы.

Другим эффективным методом решения систем линейных уравнений является метод исключения неизвестных, называемый также методом Гаусса. Он состоит в том, что данная система линейных уравнений преобразуется в равносильную ей систему специального вида, которая легко исследуется и решается.

С помощью элементарных преобразований любую систему линейных уравнений можно преобразовать так, чтобы некоторое фиксированное неизвестное , сохранившись в одном уравнении системы, исключалось из любого другого. Для этого достаточно подобрать соответствующее значение множителя 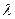для каждого уравнения, из которого выбранное неизвестное исключается. Такое преобразование системы линейных уравнений называется исключением неизвестного .

Пример 9. Решить систему линейных уравнений:

Примем за первое ведущее уравнение первое уравнение системы, за первое ведущее неизвестное – 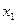; первым ведущим элементом будет . Исключим 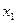из 2-го и 3-го уравнений, прибавив к ним ведущее уравнение, умноженное соответственно на и . Получим:

За второе ведущее уравнение примем второе уравнение системы, а за второе ведущее неизвестное – , вторым ведущим элементом будет . Исключим из третьего уравнения, получим: