Определение: Точка 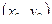 называется точкой максимума функции
называется точкой максимума функции 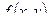 , если всюду в некоторой окрестности этой точки
, если всюду в некоторой окрестности этой точки 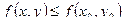 .
.
Определение: Точка 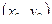 называется точкой минимума функции
называется точкой минимума функции 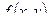 , если всюду в некоторой окрестности этой точки
, если всюду в некоторой окрестности этой точки 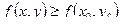 .
.
Точки максимума и минимума функции называются её точками экстремума. Значения функции в точках максимума и минимума называются соответственно максимумами и минимумами, или, короче, экстремумами, этой функции.
Необходимые условия экстремума функции двух переменных:
Если функция 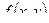 в точке
в точке 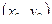 имеет экстремум, то в этой точке либо обе её частные производные первого порядка равны нулю:
имеет экстремум, то в этой точке либо обе её частные производные первого порядка равны нулю: 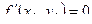 ,
, 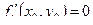 , либо хотя бы одна из этих частных производных не существует.
, либо хотя бы одна из этих частных производных не существует.
Будем называть критическими точками функции 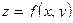 точки, в которых обе частные производные первого порядка одновременно равны нулю или хотя бы одна из этих производных не существует.
точки, в которых обе частные производные первого порядка одновременно равны нулю или хотя бы одна из этих производных не существует.
Экстремумы функции в данной области являются её критическими точками. Однако не всякая критическая точка функции будет её точкой экстремума. Для нахождения экстремумов функции в данной области надо всякую критическую точку функции в этой области подвергнуть дополнительному исследованию.
Наиболее употребительные достаточные условия экстремума для функции двух переменных формируются следующим образом:
Пусть в окрестности критической точки 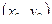 функция
функция 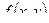 имеет непрерывные частные производные до второго порядка включительно. Рассмотрим выражения
имеет непрерывные частные производные до второго порядка включительно. Рассмотрим выражения
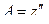 ,
,  ,
, 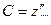 .
.
Тогда:
1) если  , то в точке
, то в точке 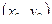 функция
функция 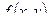 имеет экстремум:
имеет экстремум:
максимум, если 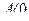 , и минимум, если
, и минимум, если 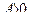 ;
;
2) если 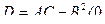 , то в точке
, то в точке 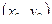 функция
функция 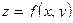 экстремума не имеет.
экстремума не имеет.
В случае, когда  , экстремум в точке
, экстремум в точке 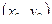 может быть, может и не быть. В дальнейшем будем называть
может быть, может и не быть. В дальнейшем будем называть 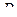 – дискриминантом.
– дискриминантом.
Пример 4. Найти экстремумы функции 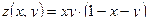 . Данная функция определена повсюду.
. Данная функция определена повсюду.
Найдем её производные первого и второго порядков.
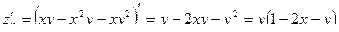 ,
,
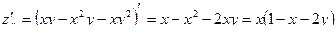 ,
,
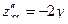 ,
,
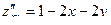 ,
,
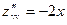 .
.
Для определения критических точек функции решаем систему уравнений:
 т.е.
т.е. 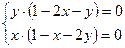
Она равносильна совокупности двух систем уравнений:
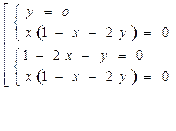
Получаем токи 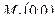 ,
, 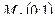 ,
, 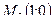 ,
, 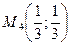 .
.
Частные производные второго порядка
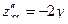 ,
, 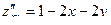 ,
,  – непрерывны всюду.
– непрерывны всюду.
Для каждой критической точки вычисляем соответствующее значение дискриминанта:
1) 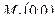 :
: 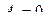 ;
;  ;
; 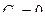 ;
; 
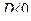
В точке 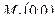 экстремума нет.
экстремума нет.
2) 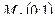 :
: 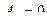 ;
; 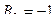 ;
;  ;
; 
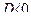
В точке 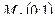 экстремума нет.
экстремума нет.
3) 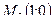 :
:  ;
; 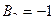 ;
; 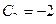 ;
; 
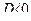
В точке 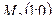 экстремума нет.
экстремума нет.
4) 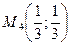 :
: 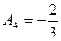 ;
; 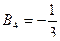 ;
; 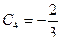 ;
; 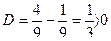
В точке 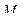 функция имеет экстремум.
функция имеет экстремум.
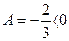 ,
,  – точка максимума. Исследуя функцию на экстремум, мы нашли четыре критические точки, из которых лишь одна является точкой экстремума. Было установлено, что в этой точке функция имеет максимум, причем
– точка максимума. Исследуя функцию на экстремум, мы нашли четыре критические точки, из которых лишь одна является точкой экстремума. Было установлено, что в этой точке функция имеет максимум, причем
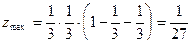 .
.
Пример 5. Фирма производит товар двух видов в количествах  и
и  . Задана функция полных издержек
. Задана функция полных издержек 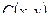 . Цены этих товаров на рынке равны
. Цены этих товаров на рынке равны 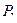 и
и 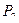 . Определить, при каких объемах выпуска достигается максимальная прибыль, найти эту прибыль.
. Определить, при каких объемах выпуска достигается максимальная прибыль, найти эту прибыль.
Решение:
Пусть 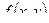 – функция прибыли, тогда
– функция прибыли, тогда
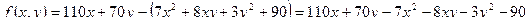 .
.
Найдём первые частные производные функции 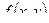 :
:
 ;
; 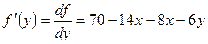 ;
;
Найдём критические точки графика функции 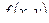 . Для этого решим систему:
. Для этого решим систему:
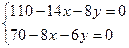


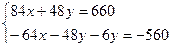
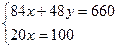
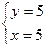
Следовательно 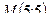 – критическая точка. Проверим её на экстремум, для этого введем обозначения:
– критическая точка. Проверим её на экстремум, для этого введем обозначения: 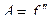 ,
, 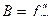 ,
, 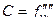 , тогда
, тогда  ,
,  ,
,  , дискриминант
, дискриминант 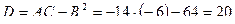 . Т.к.
. Т.к. 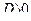 , то экстремум есть, а т.к.
, то экстремум есть, а т.к. 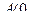 , то это максимум.
, то это максимум.
Следовательно, при объемах выпуска 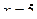 и
и  , достигается максимальная прибыль равная:
, достигается максимальная прибыль равная:

 достигается при объёмах выпуска
достигается при объёмах выпуска 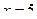 и
и 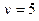 .
.
 2020-10-12
2020-10-12 146
146








