2020-10-12
124
Пусть функция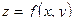 
задана в некоторой окрестности точки 
, кроме, быть может, самой этой точки.
Определение: Если для последовательности точек 
, 
,..., 
, окрестности, сходящейся к точке 
, соответствующая последовательность знаний функций 
, 
,..., 
, имеет пределом одно и то же число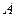 
, то это число 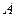называют пределом функции 
при 
, 
и пишут 
.
Геометрически тот факт, что число 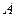является пределом функции 
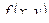при , означает, что, какова бы ни была последовательность точек плоскости 
, 
,..., 
неограниченно приближающихся к точке 
, последовательность аппликат соответствующих им точек поверхности, изображающей функцию 
имеет пределом число 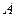. Предел функции 
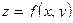при , определяется поведением функции вблизи точки 
и не зависит от значения функции в самой этой точке.
Функция 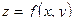, определенная в некоторой окрестности точки , называется непрерывной в этой точке, если 
Пример 1: Найти пределы:
а. 
б. 
в. 
г. 
Частные производные, градиент, дифференциал
Определение: Частными производными 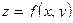по 
и по 
называются пределы вида:
Вычисление частных производных по (по ) от конкретных функций производится по известным для функций одной переменной правилам, так как частная производная функции 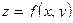, рассматриваемой как функции одной переменной (соответственно ) при постоянном значении другой переменной.
Определение: Дифференциалом функции 
называется сумма произведений частных производных этой функции на приращения независимых переменных 
или 
, учитывая, что 
, 
.
Производной 
по направлению 
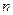функции 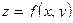называется предел 
. Производная по направлению может быть выражена через частные производные по формуле , где единый вектор 
задает направление / 
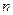углами 
и 
, образуемые с осями координат.
Определение: Градиентом функции 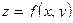называется вектор с координатами 
, 
в точке 
.
По определению 
Пример 2. Найти частные производные функций
а) 
При дифференцировании по считаем постоянной величину : 
При дифференцировании по , следовательно, 
б) 
Четные производные 1го порядка имеют вид 
, 
.
Частные производные по и по от функций 
и 
второго порядка от функции 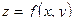в этой точке и обозначаются следующим образом:
,
,
,
,
Частные производные второго порядка зависят от координат точки, в которой они вычисляются, т.е. в свою очередь, являются функциями двух переменных, определенными в области 
или в её части.
Смешанные частные производные данной функции, отмечающиеся лишь последовательностью произведенных дифференцирований, совпадают друг с другом.
Пример 3. Найти частные производные II порядка для функции 
.
Находим производные I порядка по и по :
,
.
Найдем частные производные II порядка:
, 
,
и 
.
Теорема: Если в некоторой окрестности точки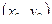 
функция 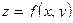имеет частные производные 
и 
и эти производные непрерывны в самой точке 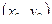, то они в этой точке равны:
.
