Степенные ряды. Интервал сходимости степенного ряда

Определение: Степенным рядом называется ряд 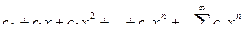(1), где коэффициенты степенного ряда. Если допустить только действительные значения для коэффициентов ряда и переменной, то получим степенной ряд в действительной области, или действительный степенной ряд.

Ряд вида так же является степенным, так как сводится к данному ряду (1) с помощью замены переменной .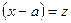

Определение: Областью сходимости степенного ряда называется совокупность тех значений при которых степенной ряд сходится. Число 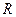– такое число, что при 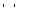– ряд сходится, а при 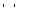– расходится, называется радиусом сходимости степенного ряда.

Интервал называется интервалом сходимости степенного ряда. При 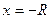, ряд может, как сходится, так и расходиться. Радиус сходимости степенного ряда может быть найден по формуле: . Для степенного ряда вида радиус сходимости находится по формуле , а интервал сходимости из условия , т.е. имеет

вид: .

Пример 16. Найти области сходимости степенного ряда

Найдем радиус сходимости ряда , т.е. интервал сходимости ряда .

Выясним поведение ряда на концах интервала сходимости. При ряд примет вид

По признаку Лейбница он сходится. При 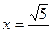получаем ряд 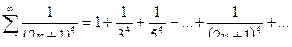. Это обобщенный гармонический ряд. Так как , то этот ряд сходится. Область сходимости данного ряда.