Характеристикой среднего значения случайной величины служит математическое ожидание.
Определение: Математическим ожиданием дискретной случайной величины называют сумму произведений всех её возможных значений на их вероятности:  .
.
Если дискретная случайная величина принимает счетное множество возможных значений, то  , причем математическое ожидание существует, если ряд в правой части равенства сходится абсолютно.
, причем математическое ожидание существует, если ряд в правой части равенства сходится абсолютно.
Математическое ожидание биноминального распределения равно произведению числа испытаний на вероятность появления события в одном испытании:  .
.
Характеристиками рассеяния возможных значений случайной величины вокруг математического ожидания, в частности, дисперсия и среднее квадратическое отклонение.
Определение: Дисперсией случайной величины Х называют математическое ожидание квадрата отклонения случайной величины от её математического ожидания:  .
.
Дисперсию удобно вычислять по формуле  .
.
Дисперсия биноминального распределения равна произведению числа испытаний на вероятности появления или не появления события в одном испытании:  .
.
Определение: Средним квадратическим отклонением случайной величины называют квадратный корень из дисперсии:  .
.
Задача 12. Два консервных завода поставляют продукцию в магазин в пропорции 2:3. Доля продукции высшего качества на первом заводе составляет 90 %, а на втором – 80 %. В магазине куплено 3 банки консервов. Найти 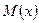 и
и 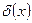 , где
, где  – число банок с продукцией высшего качества.
– число банок с продукцией высшего качества.
Решение:
Вычислим вероятность появления события 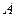 – куплена банка с продукцией высшего качества. По формуле полной вероятности имеем:
– куплена банка с продукцией высшего качества. По формуле полной вероятности имеем:
 .
.
Закон распределения дискретной случайной величины можно определить, используя формулу Бернулли:
 , где
, где  ,
,  . Случайная величина может принимать значения
. Случайная величина может принимать значения 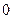 ;
; 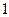 ;
;  ;
; 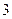 . Закон её распределения примет вид
. Закон её распределения примет вид

| 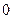
| 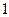
| 
| 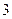
|
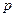
| 
| 
| 
| 
|
Тогда  ,
,
 ,
,
 .
.
 2020-10-12
2020-10-12 205
205








