Непрерывные случайные величины характеризуются тем, что их значения могут сколь угодно мало отличаться друг от друга.
Вероятность события  (где
(где 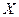 – значение непрерывной случайной величины, а
– значение непрерывной случайной величины, а  – произвольно задаваемое значение), рассматриваемая как функция от
– произвольно задаваемое значение), рассматриваемая как функция от  , называется функцией распределения вероятностей:
, называется функцией распределения вероятностей:
 .
.
Часто вместо термина «функция распределения» используют термин «интегральная функция распределения». Производная от функции распределения вероятностей называется функцией плотности распределения вероятностей или плотностью вероятности:
 .
.
Функция от распределения вероятностей выражается через плотность вероятности в виде интеграла:  .
.
Вероятность попадания случайной величины в интервал  равна приращению функции распределения вероятностей на этом интервале:
равна приращению функции распределения вероятностей на этом интервале:
 .
.
Задача 13. Случайная величина Х задана функцией распределения вероятностей




Найти плотность вероятности 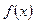 и вероятность попадания случайной величины Х в интервалы
и вероятность попадания случайной величины Х в интервалы  и
и  .
.
Решение:
Т.к.  , то
, то



Вероятности попадания случайной величины Х в интервалы вычислим по формуле:
 .
.
 .
.
 .
.
Задача 14. Плотность вероятности непрерывной случайной величины 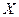



Найти функцию распределения 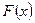 и построить её график.
и построить её график.
Решение:
 , если
, если 
 ,
,
если 
 ,
,
если  .
.



Построим график 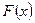 .
.
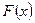
 | |||
 | |||


|


|


|
|
|
|

|
|






|

 2020-10-12
2020-10-12 161
161








